Understanding Cofactor and Cofactor Formula in Mathematics
Comprehensive Definition, Description, Examples & Rules
Introduction to Cofactor
In the field of mathematics, a cofactor is what we call a scalar entity (which has no direction) that is related to a given element in a matrix. For any given matrix A, the cofactor at let’s say a row ‘i’ and column ‘j’ is represented as Cij and is computed by taking the determinant of the submatrix created by deleting the i-th row and the j-th column and then multiplying it by (-1)^ij.
Cofactors are important components of mathematics that help in various real-life applications. It is used to compute the adjugate matrix which can be used to discern the opposite or inverse. It can also be used to find out determinants important for various calculations.
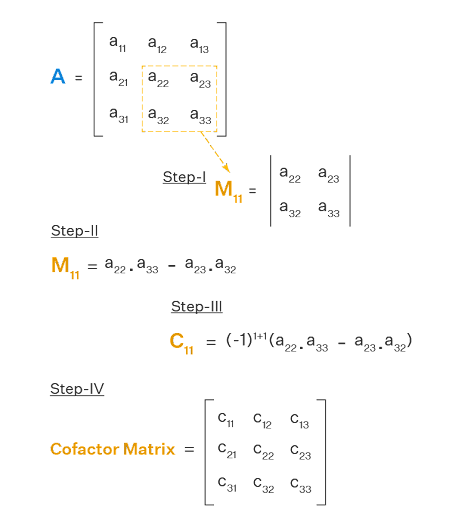
Cofactor Formula Explained:
The cofactor formula is a crucial formula of mathematics that helps us compute the cofactors of elements in a matrix in linear algebra. The cofactor formula includes various operations like discerning determinants, finding out the inverse of matrices, using Cranmer’s Rule to calculate systems of linear equations, etc. Follow the given steps to find out the cofactor of any given element a_ij in the matrix A:
- Get rid of the i-th row and the j-th column to form a submatrix.
- Find out the determinant of this submatrix, represented as Mij.
- Employ a sign according to the position of the entity. The sign will be positive if i + j is an even number and negative if it is odd.
- Finally, our cofactor is the product of the determinant of the submatrix and the sign employed in the third step.
Have a look at the example to get a clearer understanding of the concept:
Find the cofactor matrix of the matrix [ -4 11]
7 9
Solution: The matrix [ -4 11] symbolizes a 2 * 2 matrix.
7 9
For a matrix A = [ a b ],
c d
the cofactor matrix of A will be [ d -c]
-b a
Therefore the cofactor matrix of the matrix given in the question is: [9 11]
-7 -4
Cofactors in Matrix Algebra:
Cofactors have a crucial role to play in matrix algebra, for example:
- Cofactors help in computing the determinants of a matrix by adding up the products of the entities of any row or column with their related cofactors.
- Cofactors are also used in discerning the inverse or opposite of a matrix.
To find the inverse of a square matrix A, represented as A^-1 using cofactors, use the given formula:
A^-1 = 1 / det (A) * adj (A)
Here is an example of matrix operations that make use of cofactors:
Solve for A_32: 2 5 -1
( 0 3 4 )
1 -2 -5
Answer: M_32 = 2 -1
0 4
The determinant of this matrix is the product of its diagonals since the matrix is triangular.
So, (2) (4) = 8
A_32 = (-1)^3+2 (8) = -8
Applications of Cofactors:
Cofactors can be used to solve a variety of real-world problems in various fields. For example:
- Physics: Cofactors are used in physics to compute the cross product of vectors as they involve the usage of determinants, especially in electromagnetism.
- Engineering: Cofactors are used in engineering to discern the stability and safety of various kinds of structures. Since various theories in engineering are based on linear algebra, cofactors play a huge role in carrying out various operations of engineering.
- Computer Science: Cofactors are used in computer science to create graphics and images as well as the various transitions associated with them. Cofactors help technicians calculate areas and volumes efficiently and turn 2D objects into 3D easily.
Cofactor vs. Minor:
To understand the difference between cofactors and minors, we need to know that cofactors are scalar quantities that are related to a particular element in a matrix whereas minors are the determinants of a submatrix of a bigger matrix. Cofactors are majorly used in computing determinants, discerning the adjudicate matrix, and in the procedure for the inversion of the matrix. On the other hand, minors are used in the various fields of linear algebra and calculus which involves the calculation of eigenvalues, computing solutions for systems of linear equations, and in calculus which has more than one variable.
You should use cofactors mainly in problems that require finding the determinants and inverse of matrices. On the other hand, you should use minors mainly in problems that involve eigenvalues, determinants, and systems of linear equations. While cofactors and minors may be different from each other in various senses, they are also related to each other. Cofactors can be computed with the help of minors.
Cofactor Expansion:
The cofactor expansion is also known as the Laplace expansion. It is the process used for computing the determinant of a square matrix by dividing it into tinier submatrices. It works based on the idea that the determinant of a matrix can be calculated using determinants of its submatrices.
Here’s how you can use the cofactor expansion method to calculate determinants of matrices:
- Pick a row or column from the matrix which will be known as the expanding row or expanding column.
- Compute the determinant of the submatrix for each entity in the row or column that you chose.
- Find out the product of the submatrix and the related cofactor.
- Add up all the conclusions that you got in the third step.
Here is an example for you to understand the process of cofactor expansion for matrices of different sizes:
Properties of Cofactors:
The following are the different properties of cofactors:
- Cofactor expansion can be used to compute the determinant of a square matrix.
- All the elements for the identity matrix are zero except for the main diagonal, where they are all 1.
- The cofactor of an entity in the transpose of a matrix and the cofactor of an entity in the original matrix are the same.
- The adjugate matrix can be constructed using the transpose of the matrix of the cofactors.
- For a matrix with a non-zero determinant of a nonsingular matrix, the cofactor of an element is the inverse of the matrix.
Cramer's Rule and Cofactors:
Cranmer’s Rule is a process or technique in mathematics used to solve systems of linear equations with the help of cofactors and determinants. The rule gives us a way to represent solutions to problems in terms of determinants of submatrices and their related cofactors.
Here is an example of using Cramer’s Rule with cofactors:
Solve using Cranmer’s Rule:
x + y + z =6
y + 3z = 11
x + z =2 y or x – 2y + z = 0
Solution: When we write the given equation in the form of AX = B and use Cranmer’s rule, we get
x = Dx/D = 9/9 = 1
y = Dy/D = 18/9 = 2
z = Dz/D = 27/9 = 3
Infographics and Visual Aids:
Here is a visual representation to represent the cofactor formula, calculations, and its applications:
Cofactor Formula
Cofactor Calculations
Adjoint of a 2*2 Matrix
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- In the field of mathematics, a cofactor is what we call a scalar entity (which has no direction) that is related to a given element in a matrix.
- The cofactor formula helps us compute the cofactors of elements in a matrix in linear algebra.
- Cofactors and cofactor formulas are used in various fields like physics, engineering, etc.
Quiz
Question comes here
Frequently Asked Questions
The cofactor formula includes various operations like discerning determinants, finding out the inverse of matrices, using Cranmer’s Rule to calculate systems of linear equations, etc. Follow the given steps to find out the cofactor of any given element a_ij in the matrix A:
- Clear out of the i-th row and the j-th column to form a submatrix.
- Find out the determinant of this submatrix, represented as Mij.
- Employ a sign according to the position of the entity. The sign will be positive if i + j is an even number and negative if it is odd.
- Finally, our cofactor is the product of the determinant of the submatrix and the sign employed in the third step.
Have a look at the example to get a clearer understanding of finding a cofactor in a matrix:
Find the cofactor matrix of the matrix [ -4 11]
7 9
Solution: The matrix [ -4 11] symbolizes a 2 * 2 matrix.
7 9
For a matrix A = [ a b ], the cofactor matrix of A will be [ d -c]
c d -b a
Therefore the cofactor matrix of the matrix given in the question is: [9 11]
Cranmer’s Rule is a process or technique in mathematics used to solve systems of linear equations with the help of cofactors and determinants.
The following are the different properties of cofactors:
- Cofactor expansion can be used to compute the determinant of a square matrix.
- All the elements for the identity matrix are zero except for the main diagonal, where they are all one.
- The cofactor of an entity in the transpose of a matrix and the cofactor of an entity in the original matrix are the same.
- The adjugate matrix can be constructed using the transpose of the matrix of the cofactors.
- For a matrix with a non-zero determinant of a non-singular matrix, the cofactor of an element is the inverse of the matrix.