Unlocking Elegance: The Enigmatic Axis of Symmetry Formula
Comprehensive Definition, Description, Examples & Rules
Understanding the Axis of Symmetry
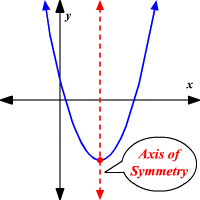
The symmetric axis or the axis of symmetry refers to an imaginary line conceived in geometry and mathematics that can divide an image or a shape into two parts that are completely identical to each other. The concept of symmetry is very important in various fields of mathematics as it helps us understand the different kinds of shapes better, ease up calculations and theories, along with helping us know and understand quadratic equations more efficiently. The axis of symmetry can also be seen in concepts apart from mathematics and geometry, and in the real world like architecture where it is needed to design symmetrical structures for maintaining the right order and foundation, and engineering to develop structures like roads and bridges that are fundamentally symmetrical and hence, strong.
The Formula for the Axis of Symmetry
Here is a representation of the axis of symmetry formula that helps us find the symmetrical axis in various situations:
For a quadratic equation of the form f(x) = ax^2 + bx + cx, the axis of symmetry can be found using:
x = -b / 2a
Description of the variables employed in the formula:
- a: Coefficient of the quadratic term
- b: Coefficient of the linear term
- c: Constant term
- x: Axis of symmetry
Equation for the Axis of Symmetry: Derivation and Application
The given axis of symmetry equation can be employed to figure out the symmetrical axis in different scenarios:
x = -b / 2a
This equation can be used for a variety of applications like:
- Computing quadratic equations
- Locating the symmetrical axis in different types of geometrical shapes.
- Discerning the various calculus functions and curves.
- Designing symmetrical buildings, bridges, arches, etc.
- Achieving a balance in various statistical reports
How to Determine the Axis of Symmetry
Here is a detailed process of steps you need to take to find out the axis of symmetry in different shapes and functions:
- Quadratic Functions
For a quadratic equation of the form f(x) = ax^2 + bx + cx, the axis of symmetry can be found using: x = -b / 2a. To find the value of x,
Note the values for a, b, and c from the provided information.
Employ these values in the formula.
Compute and simplify the equation for x.
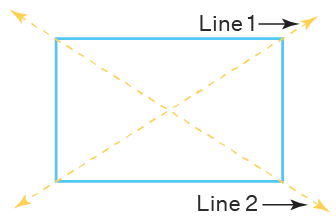
- Rectangles
For rectangles, the symmetrical axis or the line that passes through the center of the rectangle will always coincide with the longer side of the rectangle.
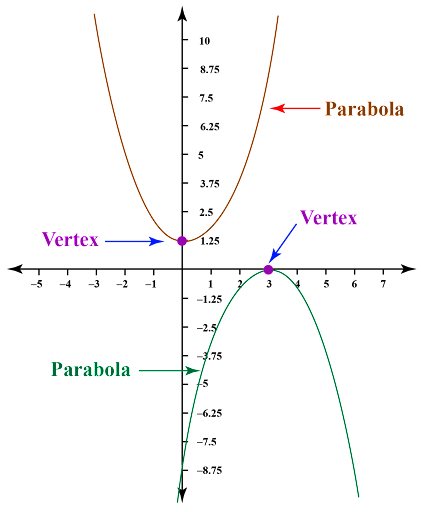
- Parabolas or Conic Sections
For a parabolic equation of the form y = ax^2 + bx + cx, the axis of symmetry can be found using: x = -b / 2a. To find the value of x,
Note the values for a, b, and c from the provided information.
Employ these values in the formula.
Compute and simplify the equation for x.
The axis of symmetry for conic shapes or parabolas will always be vertical and pass through the vertex.
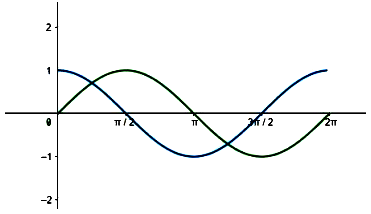
- Curves and Functions in Calculus
For functions of calculus like y = sin (x) or y = cos (x), the y-axis acts as the symmetrical axis itself because these functions are symmetrical along the y-axis.
Symmetric Axis in Geometry
The concept of the symmetric axis is crucial in the field of geometry as it helps us determine the line that divides any geometrical shape into two equal parts. The equally sectioned two parts, as a result, are completely identical to each other and will coincide or one would fit perfectly over the other if you overlap them.
Here is a list of different types of symmetric shapes with their axes of symmetry:
- Squares
A square has four lines of symmetry, amongst which two are diagonals of the square and the other two are perpendicular bisectors.
- Circles
A circle has an endless or infinite number of axes of symmetry passing through its center.
- Rectangles
A rectangle has two lines of symmetry, one along the longer side and the other along the shorter one.
- Equilateral Triangles
An equilateral triangle has three lines of symmetry, amongst which one is a median, one is an altitude and one is an angle bisector.
Practical Methods for Finding the Axis of Symmetry
For real-world scenarios like finding the axis of symmetry in fields like architecture, physics, etc. follow the given steps and tips carefully:
Architecture
Reduce the various architectural symmetrical shapes like domes, arches, roofs, etc. into basic geometric shapes like circles, semicircles, squares, etc. to find the axis of symmetry of various architectural elements.
Physics
Make use of the principles and rules of symmetry and finding the symmetrical axis and incorporate them in the various applications of physics to carry out accurate calculations and results.
Engineering
Visualize the various structures employed in the field of engineering as fundamental shapes found in geometry and estimate their axis of symmetry for safer and stronger engineered structures.
Statistics
Make use of various types of graphs to pictorially represent the different trends and changes seen in statistical data and reports and then determine a common point of symmetry to ensure balance and uniformity.
Axis of Symmetry in Quadratic Functions: An Example
For a quadratic equation of the form f(x) = ax^2 + bx + cx, the axis of symmetry can be found using:
x = -b / 2a
Description of the variables employed in the formula:
a: Coefficient of the quadratic term
b: Coefficient of the linear term
c: Constant term
x: Axis of symmetry
Axis of symmetry example
Find axis of symmetry for a quadratic equation: f(x) = 5x^2 – 4x + 2
Solution
According to the information provided in the question, we can determine axis of symmetry with:
a= 5
b= -4
c= 2
Using the axis of symmetry formula: x = -b / 2a
x= – (-4) / 2*5
x= 4 / 10
x= 0.4
Hence, the axis of symmetry for the quadratic equation f(x) = 5x^2 – 4x + 2 is 0.4.
Applications of the Axis of Symmetry
The axis of symmetry has applications in a variety of fields we see in our everyday lives, for instance:
Architecture
Architecture makes use of the concept of the axis of symmetry all the time. It helps build safer and more robust architectural structures from symmetrical bridges and buildings to domes, arches, windows and more.
Art
The concept of the axis of symmetry is used in art to create visually appealing and beautiful patterns and designs in a variety of applications such as cloth designs, the artwork of exquisite flooring tiles, and so on.
Engineering
The axis of symmetry is commonly used in engineering practices such as maintaining the security and sturdiness of huge constructions such as towers, skyscrapers, and dams by ensuring that the weight of the material is split evenly along an axis.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The symmetric axis or the axis of symmetry refers to an imaginary line conceived in geometry and mathematics that can divide an image or a shape into two parts that are completely identical to each other.
- For a quadratic equation of the form f(x) = ax^2 + bx + cx, the axis of symmetry can be found using: x = -b / 2a
- The concept of the axis of symmetry is used in a variety of real-world scenarios like art, architecture, engineering, and more.
Quiz
Question comes here
Frequently Asked Questions
The formula for calculating the axis of symmetry in quadratic equations is x = -b / 2a.
Axis of symmetry plays a crucial role in various real-world applications like art, engineering, statistics, architecture, and more.
Symmetry is an umbrella term that denotes balance and equal division of the two parts of any shape or structure to ensure an organized distribution of elements. The symmetric axis or the axis of symmetry refers to an imaginary line conceived in geometry and mathematics that can divide an image or a shape into two parts that are completely identical to each other, or in other words, symmetrical to each other.
The axis of symmetry for a parabola denotes its vertical symmetry along with determining the x-coordinate of the vertex.
Some common misconceptions or mistakes when working with the axis of symmetry are the belief that the axis of symmetry always passes through the origin of a shape and applying the axis of symmetry formula in non-quadratic equations. Some ways to avoid these mistakes and misconceptions are always checking if the equation is quadratic before applying the axis of symmetry formula, and remembering that the axis of symmetry can fall anywhere on the x-axis, not necessarily on x=0.