Mastering the Slope Formula: A Comprehensive Guide to Slope Calculation and Interpretation
Comprehensive Definition, Description, Examples & Rules
Introduction to Slope
The slope of a line shows how steep it is and the exact way it tilts. You figure out the slope using two points on the line. To get the right slope, you do a little math: the change in Y divided by the change in X. By checking the line’s tilt from left to right, you can spot the slope. To do this, you look at the ratio of rising vs running between the two points on the line. Another name for slope is gradient. It’s a special type of number that tells us the direction and how steep the line is.
Importance
The primary importance of slope in mathematics are:
- The slope calculates how much the dependent variable shifts with every change in the independent variable.
- It displays how the Y axis, or vertical line, changes when there’s any shift in X or the horizontal line.
- Several math calculations in geographic studies determine the slope and formula, highlighting its importance in key calculations.
Real-world Significance
If you understand the slope of everyday objects, it will help you make many essential decisions. The formula of the slope is used for measuring the slope or the steepness of a line between the two points on a particular graph. Calculating the slope is very important while building roads, and understanding the road’s steepness is also essential, so you need the slope formula. A lot of different constructions require you to understand the slope.
Understanding the Slope Formula
The formula for calculating the slope is very easy, and you do not have to use a lot of components to calculate it. The basic slope formula is:
- m = ∆y/∆x
Components of Formula
Here, m is considered the slope of the line.
∆x is a change in the coordinates of the x-axis.
∆y is a change in the overall coordinates of the y-axis.
The formula for Coordinates:
- (Y2 – Y1)/(X2 – X1)
Slope Equation vs. Slope Form
The Slope equation and the slope form are the two ways you can express the formula of a slope in the form of a straight line. The slope formula directly emphasizes a slope, any point on the line. The slope form shows the slope and the y-intercept of the line.
You use the slope form when you know the slope of the line is to be examined, and the point is also given as the Y-intercept. For any other situation, you have to use the slope equation to calculate the exact slope of the line and determine the slope using the regular equation formula.
Solving Problems with the Slope Formula
You should follow the basics when calculating the problem using the slope formula. The step-by-step process that you have to follow is as follows:
- Determine the exact coordinates you will use for your mathematical calculation.
- With this determine the (X1, X2) and (Y1, Y2) of the sum.
- Use the proper slope formula example that is required.
- Determine your answer.
Examples
Using the Slope Formula determines the Slope whose coordinates are (3,7) and (5,2)
Solution:
We are using the slope formula to calculate the slope with coordinates (3,7) and (5,2)
So, (X1, X2) = (3,7) and (Y1, Y2) = (5,2)
The formula to calculate the Slope is m = (Y2 – Y1)/(X2 – X1)
So, m = 2 – 5/ 7 – 3
m = -¾
So the Slope of the line is -¾
Common Mistakes
The common mistakes that you should avoid which are confusing while calculating the Slope of a line on the graph are:
- There is a lot of confusion in determining the rise or the run of the lines, so you might mess with the coordinates and use the incorrect coordinates while calculating.
- To find the slope, you must determine the change in the vertical access and the horizontal axis between the two points of the line, and you should do it correctly.
- Interchanging the coordinates is another section where people make many mistakes, and it’s where you should avoid making mistakes.
Practical Application
The real-life scenarios where you must use the slope formula in your calculations are:
- When constructing roads, determining the road’s slope is key. To do this correctly, apply the slope formula for exact calculations.
- Snowboarders also need to consider the slopes of hills to judge the dangers and the speed of the snowboarding, for which using the formula is also essential.
- When constructing wheelchair rams, calculating the slope formula is also one of the major considerations and has an essential role to play in it.
Case Studies
The different case studies related to the slope formula are:
- Coastal Engineering Study, 2017, C Zhang, Q Zhang, J Zheng, Z Demirbilek.
- Bulletin of Engineering of Geology, 2022, RAM Nazari, A Ghanbari.
- Tailings and Mine Waste, 2022, M Pinto, S Barrera.
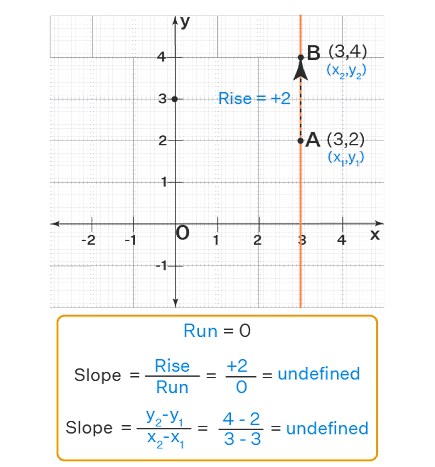
Visualizing Slope
The Interpretation of the Slope on a Graph is:
Examples of Slope Formula Application
The range of examples of the slope formula application are:
Example 1: Using the Slope Formula, determine the Slope whose coordinates are (2) and (8)
Solution:
We are using the slope formula to calculate the slope with coordinates (2) and (8)
So, (X) = (2) and (Y) = (8)
The formula to calculate the Slope is m = (Y)/(X)
So, m = 8/2
m = 4
So the Slope of the line is 4
Example 2: Using the Slope Formula, determine the Slope whose coordinates are (3,5) and (9,3)
Solution:
We are using the slope formula to calculate the slope with coordinates (3,5) and (9,3)
So, (X1, X2) = (5,3) and (Y1, Y2) = (9,3)
The formula to calculate the Slope is m = (Y2 – Y1)/(X2 – X1)
So, m = 9 – 3/ 5 – 3
m = 6/2
So the Slope of the line is 3
The application of slopes in different fields are:
- Trigonometry and Geometry: Slope helps to identify various angle slopes and to figure out the tangent values that need the slope. It’s really crucial to use the slope formula to work out shapes in geometry.
- Engineering: Engineers are the primary users of the slope formula as they must build many things, so they need to understand the slope well and use it effectively.
Snowboarding Ramps: The people who make snowboarding ramps need to check the slope accurately. This ensures the ramp is secure for snowboarders.
Special Cases
There are certain special cases where the slope calculation becomes different, and the slope formula uses a lot of special equations. These are:
- The X-axis’s slope: The Slope of X axis, or any line running alongside it, has a zero slope. This is due to the fact that the angle between this line and any other on the X-axis is also zero. No matter the formula used, the X-axis slope stays at zero. Why? Because dividing any number by zero results in zero. So, the math for the slope of the X-axis always equals zero.
- In-Slope: The In slope is the slope-intercept form of the linear equation, which is y = mx + b. This is the form of the slope that is different from its standard linear equation and identifies the slope of the line in the number before x.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Slope is one of the most essential parts of mathematical calculations, such as trigonometry and geometry calculations.
- The x-axis and y-axis are essential parts of the slope calculation. Interchanging the axis is the main area of calculating the slope.
- The slope of the x-axis or any line parallel to the x-axis is always zero due to the angle of intersection being zero.
Quiz
Question comes here
Frequently Asked Questions
The tilt of the x-axis, or any direct line parallel to it, is marked as zero. Why? Because the standards say that the angle made between a line and others on the x-axis never changes from zero. As a result, working out the slope using a standard formula isn’t an option. This is the case for any set line on the x-axis.
You can visualize a slope by just looking at the rise and the run on the graph, as the vertical change between the two points is called the rise, while the horizontal change is called the run. The slope calculation is equal to the rise divided by the run. You can easily see the slope and visualize it.
There are common mistakes that are essential for you to avoid if you are using the slope of the line on a graph. These are:
- Not understanding the rise and the run and using the wrong coordinates to calculate the slope.
- Failing to identify the vertical axis of the horizontal Axis will directly messing up the calculation.
- Interchanging the coordinates is another scenario where a lot of calculation differences happen.