Unlocking the Mysteries of Squares
Comprehensive Definition, Description, Examples & Rules
Introduction to Squares
A square is one of the geometrical shapes that is applied in an array of tasks and applications in the real world. To define square, we can say that a square is a four-sided polygon with all sides equal in length and angles measuring 90 degrees. The square has such a shape that if it is cut by a plane from the middle then both the divided sides will be symmetrical. To know what is square, go through the following most important properties of a square that make it unique from all other kinds of geometric shapes:
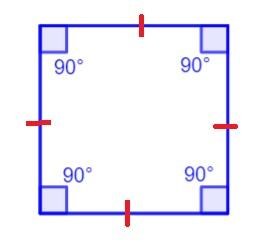
- Each of the four equal angles in the inner part of a square is a right angle, i.e. 90 degrees in value.
- Each of the four sides of a square is similar in length.
- Each pair of opposite sides in a square runs parallel to each other.
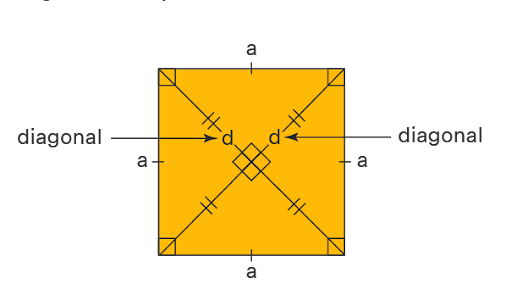
- The diagonals of a square meet each other at a right angle or an angle of 90 degrees.
- A square has two diagonals which are alike each other in length.
- There are a total of four corners or vertices in a square.
- The square’s diagonal divides it into two similar isosceles triangles.
- The length of diagonals in a square is bigger than the length of the square’s sides.
What is a Square?
The square shape is one of the most unique shapes which looks plain and simple but has copious properties that distinguish it from other geometrical shapes. In its essence, a square is a four-sided polygon, which means that it has four sides. All of these four sides are equal to each other. Additionally, the angles made at the four vertices of a square are all 90 degrees in value.
The equality in the length of the sides and the value of the angles makes the square one of the most symmetrical and regular shapes found in geometry. If you rotate a square by 90, 180, or 270 degrees, it will always align perfectly with itself. This shows that the square has a very geometrically even layout that can be used to compute problems in all walks of life. Furthermore, the angles found in the inner part of a square are equal in value. Hence, this evenness in the properties of a square makes it one of the most balanced and regular geometric shapes we know today.
The Square Formula in Mathematics
There are different square formula in maths prescribed for different calculations. Given below are the respective formulas for each:
Area of a Square
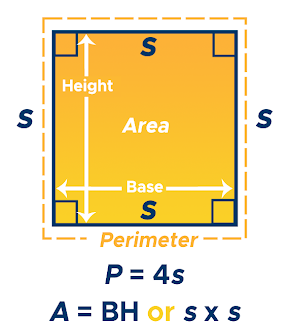
What’s the area of a square? The area of a square is the amount of space taken in by the whole of the square. Mathematically, it can be noted as:
A = s^2
Here, A connotes to Area of a square the square
s is the side of the square.
Perimeter of a Square
The perimeter of a square is the boundary covered by the sides of the square. In other words, the perimeter of a square helps us calculate the demarcation or the distance that is covered by the sides of the square. Mathematically, it can be noted as:
P = 4*s
Here, P connotes to the perimeter of the square
s is the side of the square
The diagonal of a Square
The diagonals of a square join the opposite vertices or corners of the square. Given that a square will always have four vertices or corners, there are only two diagonals in a square in total. Mathematically, it can be noted as:
d = s√2
Here, d is the diagonal of the square
s is the side of the square
Calculating the Perimeter and Area of a Square
The perimeter and area of a square are the two most crucial calculations that help in carrying out applications in everyday life. The length of the side of a square is important in both calculations. To know about the calculation of area and perimeter of a square, go through the following step-by-step explanation:
Area of a Square
The expanse covered by the square in a two-dimensional plane is its area. To know what is the area of a square, we can define it to be the square of the sides or in other words, the length of a side multiplied by itself. It is quantified in square units. Mathematically, we can represent the area of a square as:
Area per square unit = side * side
Or,
Area per square unit = side^2
Hence, if s is the length of a side of a square, its area would be A = s^2 sq. unit
Perimeter of a Square
When the lengths of all four sides of a square are clubbed together, we get its perimeter. The unit of the perimeter follows the unit in which the length of the square’s sides is mentioned. The length of the distance covered by the boundaries of a square, or its perimeter, is calculated by multiplying the length of a side of the square by four. Mathematically,
Perimeter = Side + Side + Side + Side
Or,
Perimeter = 4 * Side
Hence, if s is the length of a side of a square,
Perimeter = 4s unit
Common Uses and Applications of Squares
Squares are those geometrical shapes whose unique properties can be applied in an array of everyday applications that make our lives easier. Some of the many fields where the concept of squares and their properties are employed are:
- Tiled Floors: Squares provide our tiles and floors with symmetry and order. Flooring tiles come in the square shape to give your floors a regular and balanced look. Floor tiles that are random or quirky in shape do not look pleasing to the eye and give a very haphazard and untidy look to your home’s floors. On the other hand, square tiles make your rooms look put together and balanced.
- Picture Frames: Picture frames come in the shape of a square to attribute a sense of order and evenness to the picture. The equal sides and angles of a picture frame in square shape make the elements of the picture stand out more attractively. Unlike a haphazard frame, it does not take away attention from the specificities of the picture.
- Digital Screens: More and more digital screens are seen in the square shape. This is done to make the viewer experience better by displaying content on a screen that is regular in shape and equally leveled from all angles and sides. Unlike a haphazard digital screen which may distort parts of a movie, the balanced and regular shape of a square makes the digital videos enriching and captivating.
- City Planning: Squares are used in the process of devising the plan of cities. The uniform shape of a square helps design cities that are regular and more organized. Since a square has all four sides equal, cities based on a square plan end up being more handy than random and irregularly planned cities.
Anatomy of a Square
Have a look at the following visual representation of the properties of a square:
Length of The Side of a Square
Angles of a Square
Diagonals of a Square
Area and Perimeter of a Square
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A square is a polygon with four sides in total that are alike each other in length and four angles that are alike each other in value (each measuring 90 degrees).
- The formula for computing the area of a square is s^2.
- The formula for quantifying the perimeter of a square is 4*s.
- The formula for computing the length of a diagonal of a square is s√2.
- Squares are used in everyday applications like floor tile designs, city planning, digital screens, and more.
Quiz
Question comes here
Frequently Asked Questions
A square-based pyramid has 8 edges in total.
A square has the unique properties mentioned below:
- Each of the four equal angles in the inner part of a square is a right angle, i.e. 90 degrees in value.
- Each of the four sides of a square is similar in length.
- Each pair of opposite sides in a square runs parallel to each other.
- The diagonals of a square meet each other at a right angle or an angle of 90 degrees.
- A square has two diagonals which are alike each other in length.
- There are a total of four corners or vertices in a square.
- The square’s diagonal divides it into two similar isosceles triangles.
- The length of diagonals in a square is bigger than the length of the square’s sides.
The area of a square can be computed using the formula: A = s^2, where A is the Area of the square and s is the side of the square.