Exploring Cylinders: Shapes, Formulas, and Real-Life Applications
Comprehensive Definition, Description, Examples & Rules
Introduction to Cylinders
The cylinders definition is a three-dimensional shape. It has two parallel circular bases, and the joining of the shape is a curved safe. In geometry, the center of the circular bases overlaps each other, which helps to form a right cylinder. The line segment joining the two centers of the cylinder is the axis, and it denotes the height of the cylinder. A cylinder is a perfect 3D geometrical shape, a prism with a circle in its base. A cylinder is a perfectly upright shape with special structures in it.
Cylinder Shape and Characteristics
The cylinder shape is a 3D shape that consists of a parallel circular base and is directly joined through a curved surface. The defining characteristics of a cylinder shape include:
- It has a curved lateral surface and flat faces, and all these surfaces are identical.
- It consists of two circular forms of basis, which allows the cylinder to stand straight.
- The line segment that joins the two circular bases from the center is known as the access, which also denotes the height of the cylinder shape.
Visual Representation of Cylinder Examples
Cylinder Formula
All the 3D shapes in geometry consist of a minimum of two primary formulas: the volume and the surface area. The shape cylinder consists of three major formulas that you have to use for calculating the volume and surface area. The formula includes:
Volume
The formula for volume of a cylinder is:
- πr²h
Total Surface Area
The formula that you have to use for calculating the total surface area of a cylinder is:
- 2πr (h+r)
Curved Surface Area
The formula for calculating the lateral surface area of the curved surface area of the cylinder is:
- 2πr
The uses of this formula for different types of cylinders include:
- For all these calculations, you must determine the value of ‘h’ and ‘r’ in the formula.
- ‘h’ is the total height of the cylinder, while ‘r’ is the circular radius of the cylinder’s base.
- For calculations of all cylinders, the value of π(pie) is 22/7 or 3.14.
- After these, the calculations for all cylinders are similar, and you use the exact formula to make accurate calculations.
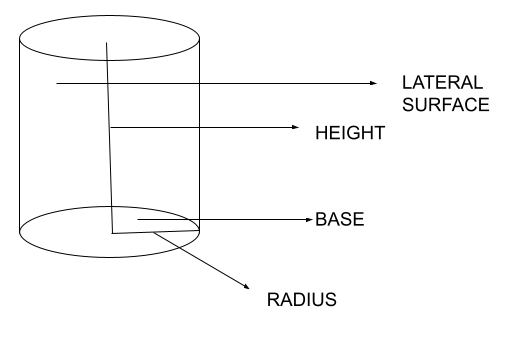
Parts of a Cylinder
Various components of a cylinder help to make accurate calculations of a cylinder. The exact components of a cylinder include:
Base
The base of the cylinder is circular and is one of the essential parts of the cylinder. There are two circular bases of a cylinder connected through a rectangular area with edges, and the base of the cylinder is an actual circle.
Height
The height of the cylinder is the exact distance from the center of one base of the cylinder to the other base. The circle’s height is in the form of an axis and is highly important in calculating the surface area and volume.
Radius
The radius of the cylinder is calculated as the radius of the circular base of the cylinder. Both the bases of the cylinder are a perfect circular shape that is equal, so the radius of both these bases is the same.
Lateral Surface
The lateral surface area of the cylinder is the exact area that is calculated, excluding its base. It is the reason for the cylinder’s rectangular area that must be determined as the lateral surface area.
Diagram
Equation of a Cylinder
Two primary mathematical equations of the cylinder are essential for calculation. These two mathematical equations include the calculation of the volume of the cylinder and the calculation of the total surface area of the cylinder. These mathematical equations include:
- Volume: πr²h
- Surface Area: 2πr (h+r)
There is another mathematical equation that is related to the cylinder formula, and it is the calculation of the lateral surface area excluding the bases.
All these mathematical equations have a primary role in the cylinder’s geometry. The exact geometrical calculation of the shape is possible when it is directly related to the mathematical equations of the shape.
Real-Life Examples of Cylinders
There are many everyday 3D cylinder shape examples that we use. The examples of cylinders in real life are:
- Soda Cans: These are the most used 3D cylinder shape items in our day-to-day life and are a perfect example of a cylinder shape.
- Pipes: These are available in various shapes and sizes, and the lengths of these also differ, but most pipes are available in cylindrical shape. The bathroom pipes are a perfect example to define this.
- Batteries: These are also available in different shapes and sizes; if you want to be precise, these are also available in cylindrical shapes.
There are many industries in which the cylinder shape has a primary role. Many mathematical calculations happen through the cylinder shape, but one of the primary areas it focuses on is the water bottle and can industries. Beverages are offered in cylindrical shapes, and deodorants are available in cylindrical shapes, making the chemicals inside them long-lasting.
Volume of a Cylinder
The formula that you use for calculating the volume of a cylinder is:
- Πr²h
Here, ‘r’ is the radius of the base of the circle while ‘h’ is the exact height of the cylinder from one base center to the other base center. The value of pi can be taken as 22/7 or 3.14. You have to follow these steps for all types of cylinder volume calculations. The volume of a cylinder is always expressed in cubic units.
Examples
Calculate the Volume of a Cylinder with a radius of 3 cm and a height of 10 cm \
The formula is:
Πr²h
So,
π × 3² × 10
22/7 × 90
282.86
So, the volume of the cylinder is 282.86 cm³.
For decimal points, you must take two digits after the decimal and use the exact decimal rule to establish the answer.
The surface Area of a Cylinder
For calculating the total surface area of a cylinder, the direct formula is:
- 2πrh + 2πr²
The simplification is:
- 2πr (h + r)
The properties for calculating the surface area are similar. The surface area of a cylinder is denoted in square units.
Example
Calculate the Surface Area of a Cylinder with a radius of 5 cm and a height of 12 cm
The formula is:
2πr (h + r)
2×22/7×5 (12 + 5)
534.29
So, the surface area of the cylinder is 534.29 cm².
Cylindrical Prisms vs. Cylinders
There is a major difference between a cylinder shape and a cylindrical prism. A cylinder is a shape that consists of two flat ends with an occurring surface, while on the other hand, the prism contains two polygons for the two ends, and the remaining part of the prism is the plane rectangular faces. The major characteristics of both these shapes are that a cylinder does not have any diagonals, while a prism contains a variety of diagonals.
Properties of Cylinders
The primary properties of the cylinders are:
- There is a constant slice of a cylinder through a circle, so the cylinder has a cross-section area formula that can be divided by 2 for the calculation.
- There is a constant relationship between the height and the radius of the cylinder as the height is calculated from the exact point of radius of one base to the other.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A cylinder is one of the most important 3D shapes.
- The volume and surface area of the cylinder can be calculated by using its radius and height.
- There is a primary difference between a cylinder and a cylindrical prism.
- The surface area and cylinder volume formula in Hindi and English is available on Edulyte.
Quiz
Question comes here
Frequently Asked Questions
There are wide areas in which we use the cylinder shape, and these are:
- Soda Cans
- Water Bottles
- Batteries
- Candles
- Pipes
- Gas Cylinders
- Fire Extinguisher
A cylinder is a two-flat surface shape, while a prism has two polygons at its ends. A cylinder does not consist of a diagonal, while on the other hand, a prism consists of a lot of diagonals.
The mathematical equation of the cylinder is directly related to its geometry as the volume of the cylinder is expressed in cubic units geometry through its mathematical calculation. In contrast, the surface area of the cylinder is expressed in cube square units through its mathematical calculation.
The primary characteristics of a cylinder are:
- It consists of two parallel circular bases.
- The reason for the cylinder is a curved surface.
- The perpendicular distance from one base to the other base of the cylinder is known as the height of the cylinder. It is also known as the axis of the cylinder.