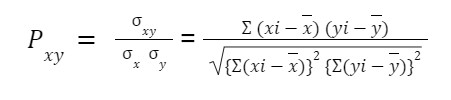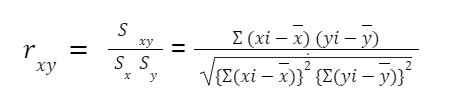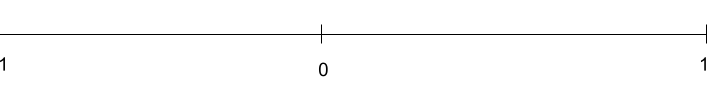Understanding Correlation Coefficients: Formulas, Definitions, and Examples
Comprehensive Definition, Description, Examples & RulesÂ
Introduction to Correlation Coefficients
The correlation coefficient definition is a number between minus 1 and 1, telling you the direction and strength of the relationship between the variables. It helps you to reflect on how similar the measurement of two or more variables across a particular data set is. It helps you to define the linear correlation coefficient between the degree of relationship between two or more variables and the degrees denoted by ‘r.’ The primary example of using the correlation coefficient in day-to-day life is when calculating the performance of two stocks that move in a particular direction and are positive.Â
Correlation Coefficient Formula
The formula for the correlation coefficient is denoted in different ways and requires a lot of statistical calculation. There are two types of formulas for calculating the correlation Coefficient: the population formula and the sample correction formula.
Population Formula
The population correlation formula is:
x y is the population standard deviation of the formula.
xy is the population covariance in the formula.
x, y is the population mean in the formula.
Sample Correction Formula
The sample correction correlation Coefficient formula is:
Sx Sy is the population standard deviation of the formula.
Sxy is the population covariance in the formula.
x, y is the population mean in the formula.
Types of Correlation Coefficient
There are various types of coefficient of correlation that you have to calculate, and these types of correlation Coefficient are:
Pearson Correlation Coefficient
The Pearson correlation coefficient is a coefficient that helps measure the linear correlation between two data sets. It is the most common way of expressing the coordination coefficient and linear correction. It measures the direction and strength between the variables in the most simple ways. It is denoted in the form of ‘r.’Â
Spearman Rank Correlation Coefficient
It is the non-parametric measure of rank correlation, which is the statistical dependence between the rankings of two variables. It provides the direct relationship between these two variables when statistics are used and is often denoted by the Greek letter (rho). It has the primary role in data analysis.Â
Kendall’s Tau Correlation Coefficient
Kendall’s Tau Correlation Coefficient is the similarity of the orderings of the data when each of its quantities ranks them. It is also a non-parametric measure of association based on the number of concordances and discordances in the paired observation.
Correlation Coefficient Range
coefficient can never be zero, as it will mean there is no correlation coefficient for the data set. The interpretation of the result for the correlation coefficient depends upon the range in which the value falls.
Visual Representation
Interpreting Correlation Coefficient
You should check the value of the correlation Coefficient, which will help you to indicate the strength and direction of the relationship of the correlation coefficient. The closure of the correlation coefficient value is that the last one, the higher the strength of the data set, while it reduces when the direction is moving forward to – 1. The linear relationship between these variables is calculated using the correlation Coefficient values.Â
The examples of the correlation coefficient interpretation of the values are the primary when determining the performance of the stock as the correlation coefficient closer to the positive value, the better performance of the stock, while the negative value indicates that the stock is performing negatively.Â
Correlation vs. Causation
The correlation among the variables is not the change in the mean in one variable; it is the cause of the change in the values of the other variable. On the other hand, causation indicates that a particular event results from the occurrence of the other event. The correlation does not imply causation.Â
The importance of not inferring causation from correlation alone is:
- It serves as a useful reminder of how you think about the relationship of two variables, y and x.
- It might result from the random chance while the variables appear to be related, but there is no particular underlying relationship.Â
- Causation is possible without correlation when a lack of change exists among the variables.Â
Correlation vs. Causation
The correlation among the variables is not the change in the mean in one variable; it is the cause of the change in the values of the other variable. On the other hand, causation indicates that a particular event results from the occurrence of the other event. The correlation does not imply causation.Â
The importance of not inferring causation from correlation alone is:
- It serves as a useful reminder of how you think about the relationship of two variables, y and x.
- It might result from the random chance while the variables appear to be related, but there is no particular underlying relationship.Â
- Causation is possible without correlation when a lack of change exists among the variables.Â
Correlation Coefficient Calculation
The step-by-step instructions on how to calculate the correlation Coefficient using the formula are:
- Count the exact number of data points.
- Find the Values of the x and y data sets and calculate the sum of these products.
- Find the sum of these values.Â
Correlation Coefficient Example and Calculations
Given the following population data. Find the correlation coefficient between x and y for this data. (Take 1√7 as 0.378)
x | 600 | 800 | 1000 |
y | 1200 | 1000 | 2000 |
Solution:
To simplify the calculation, we divide both x and y by 100.
x/100 | y/100 | xi - x | yi - y | (xi-x)2 | (yi - y)2 |
|---|---|---|---|---|---|
6 | 12 | -2 | -2 | 4 | 4 |
8 | 10 | 0 | -4 | 0 | 16 |
10 | 20 | 2 | 6 | 4 | 36 |
8 | 14 |
Using the formula:
16/ √8 √56 = 2/√7 = 0.756
The correlation Coefficient is 0.756
Correlation Coefficient in Statistics
The primary significance of the correlation coefficient formula in statistics and data analysis is:
- Statistical calculation tells the strength and direction of the linear relationship between the x-axis and the y-axis.Â
- The reliability of the linear model of the data analysis depends upon the observation of data points, which is the primary role it plays in data analysis.Â
- Indicates the strength of the linear relationship between the two variables and exactly denotes the variable’s performance.Â
The role of the Coefficient in particular areas is as follows:
- Regression Analysis: The overall regression analysis becomes very easy when using the correlation coefficient equation, and it is one of the primary areas where analysis occurs.
- Hypothesis testing: The calculation of hypothesis testing becomes very easy, and it is one of the most exact areas where the correlation Coefficient plays a good role.Â
- Predictive Modeling: Making future prediction modules becomes very easy while using the coordination Coefficient formula, and it is one of the most active areas where the correlation of Coefficient is happening.
Correlation Coefficient Research
The primary usage of the correlation Coefficient in different fields of research are:
- Social science: The calculation and data analysis in the research field of Social Science requires using a correlation Coefficient to execute the result of the research and find the exact values required during the research.Â
- Economics: Many economic calculations are important and require a correlation Coefficient to determine the economic data of these calculations.Â
- Epidemiology: It requires the correlation Coefficient calculation and utilizes the function very well to determine the performance of the variables in epidemiology.
The research studies that used the correlation analysis in it are:
- Correlation analysis importance and usage by EA Curtis
- Requirements of correlation Coefficient by P Ahlgren
- Correlation analysis in biological studies by S Yadav
Common Misinterpretations
There are certain misinterpretations that are directly related to the correlation coefficient. These include:
- There is a direct misconception that there is a relationship between the two variables, which means causation.Â
- There is one variable that causes changes in the other variable, which is the misconception.Â
- There is a particular tendency to meet this casual error when the two variables are related.Â
To avoid the statistical pitfall in Coefficient, you should always use the scatter plots as the different graphical tools to visualize the data and then check the non-linear patterns.
Limitations of Correlation Coefficients
There are certain limitations of the correlation analysis, and these are:
- One of the limitations of the correlation Coefficient assumes a linear association and is inaccurate.Â
- It also leads to the linear transformation, and the transformation of either x or y will not affect the correlation coefficient.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!
Key Takeaways
- The correlation coefficient is not an accurate value calculation.Â
- There are certain misconceptions related to the correlation Coefficient, which makes it difficult to calculate.
- You might use two formulas to calculate the correlation Coefficient formula.
Quiz
Question comes here
Frequently Asked Questions
A positive correlation coefficient means that the prediction for the variable is perfect, and the relationship among the variables is very good.Â
A negative correlation coefficient means that the perfection of the variable and the data set is negative, and it is wrong to choose the particular data variable or the particular data set.Â
The correlation coefficient of zero means the correlation coefficient does not exist, as it is impossible for the value of the correlation coefficient to ever be zero.Â
No, a correlation coefficient can never prove causation. It cannot say anything about the effect and cause relationship, and the conclusion of the two variables is not possible in this scenario.Â
Common misinterpretations of correlation Coefficient are:
- One variable can cause a change in another variable, which is one of the biggest misconceptions.Â
- There is a relation between the tooth variables through the means of causation.
- There is a particular tendency to meet the casual error received through its related variables.Â
