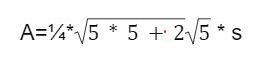Pentagon Area Unveiled: Formulas, Methods, and Real-World Applications
Comprehensive Definition, Description, Examples & Rules
Introduction to Pentagons and Area Calculation
A polygon with five sides, five angles, and five vertices is known as a pentagon. It is an important geometrical shape naturally found in nature (for example, flowers’ petals) and frequently used in various man-made structures like logos, signs, architectural designs, etc. All the interior angles inside a regular pentagon sum up to 540 degrees, and each angle in a regular pentagon measures up to 108 degrees.
In geometry, pentagons are one of the most basic polygons which act as building blocks for more complex shapes. The symmetry of a pentagon comes in handy in various concepts in life like art, design, architecture, etc. In architecture, pentagons design buildings, rooms, decorative elements, etc. In carpentry and woodwork, pentagons are used in various projects to cut and fit pieces accurately. Moreover, a pentagon’s area is needed to determine the materials needed for structural stability in engineering and construction.
The Formula for Finding the Area of a Pentagon
The formula for calculating the area of a regular pentagon (A) with side (s) is represented as
Here,
s represents the side length of the pentagon, which is used to calculate the area based on the regularity of the shape.
The square of s or s^2 ensures that the area calculation represents the relationship between the side length and the area in a regular pentagon.
The constant terms ⅕,√5, and 5+2√5 ensure that area calculations are accurate for regular pentagons.
Calculating the Area of a Regular Pentagon
Here is the step-by-step process of how to calculate the area of a regular pentagon(A), with examples:
To calculate the area of a regular pentagon, you can use the formula:
A=¼*n*s^2*cot(π/n)
Where
‘n’ stands for the number of sides in a pentagon, which is 5 for a regular pentagon.
‘s’ represents the length of one side.
To calculate the area of a regular pentagon, follow the given steps:
Step 1: Measure the length of one side of the regular pentagon.
Step 2: Place the value of ‘n’ (equal to 5 for a regular pentagon) and ‘s’ in the formula above.
Step 3: find the cotangent of π/5.
Step 4: Calculate the area using the values obtained through steps 2 and 3.
Example:
Consider a regular pentagon with a length of side 10 units. Calculate its area.
Solution:
It is given that, ‘s’=10 units
We know that, ‘n’=5 for a regular pentagon
So, so the area of this regular pentagon would be: A=¼*n*s^2*cot(π/n)
A= ¼*5*10^2*cot (π/5)
cot (π/5)=1.3764 (approximately)
Hence, A=¼*5*10^2*1.3764
A=172.05 units
Types of Pentagons
Pentagons can be of varied forms and varieties. The two most basic forms of pentagon are regular and irregular pentagons:
Regular Pentagon
A regular pentagon is a polygon with 5 sides that are equal in length and also have 5 equal angles. All the 5 angles inside a regular pentagon measure 108 degrees each. These pentagons are highly symmetrical because of the symmetry and uniformity in side lengths and angles.
Irregular pentagon
On the other hand, irregular pentagons are polygons with 5 sides of different lengths and angles of varying measures. In irregular pentagons, neither the sides nor the angles are of equal measure and they lack the high degree of symmetry seen in regular pentagons.
Some other types of pentagons are also found, for example:
Convex Pentagon
A pentagon in which all internal angles are less than 180 degrees is called a convex pentagon. The sides of a convex pentagon do not cross over each other.
Concave Pentagon
A concave pentagon has at least one internal angle greater than 180 degrees, and its sides may cross over each other, creating a cave-like appearance.
Area of an Irregular Pentagon
Unlike a regular pentagon which has a defined formula for calculating its area, an irregular pentagon’s area can be calculated in a variety of ways:
- Dividing the pentagon into triangles and trapezoids and calculating their areas to sum them all up and find the total area of the pentagon.
- Dividing the pentagon into rectangles and triangles and calculating their areas to sum them all up and find the total pentagon area.
- Dividing the pentagon into smaller and manageable shapes and calculating areas of individual shapes to sum them all up and find the total pentagon area.
- Calculating the approximate area of the pentagon by drawing grids inside the pentagon and multiplying the total number of full squares inside the pentagon by the area of one full square.
Rectangular Pentagons
A “rectangular pentagon” is defined as a house-shaped, integer-sided convex planar figure composed of a triangle with base B and sides u and v surmounting a rectangle with width B and height d. The triangular portion’s sides u and v can be switched without changing the area or perimeter of the pentagon.
Unlike a regular pentagon in which all angles are equal to 108 degrees, a rectangular pentagon is an integer-sided convex pentagon with the additional constraint that two non-adjacent sides have identical lengths and form a right angle with the intervening side.
By convention, the area of an equable rectangular pentagon is an integer, as is the area of its rectangular part; hence the triangle is Heronian by subtraction. The area of a rectangular pentagon can be defined as
A = AT + Bd = PT + 2d = P
Where AT and PT are the triangular portion’s integer area and perimeter.
Properties of Pentagons
Pentagons have various properties that define them and make them unique. Some of these properties are:
- There are five sides in a pentagon.
- There are five angles in a pentagon.
- All sides are of equal lengths and all angles are of equal measures in a regular pentagon.
- We get to see a rotational symmetry that is fivefold, in a regular pentagon. If a regular pentagon is rotated by 1/5th of a complete turn, it will end up in the same position in which it started rotating.
All of these properties come in handy when calculating the area. For example:
- Calculations dealing with regular pentagons are easier as all the sides and angles are equal.
- Knowledge of computing areas of different shapes is necessary to compute the area of irregular pentagons.
- Symmetry can play a crucial role in finding out the area of irregular pentagons.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A polygon with five sides, five angles, and five vertices is known as a pentagon.
- A regular pentagon is a polygon with 5 sides that are equal in length and also have 5 equal angles.
- On the other hand, irregular pentagons are polygons with 5 sides of different lengths and angles of varying measures.
- To calculate the area of a regular pentagon, you can use the formula: A=¼*n*s^2*cot(π/n)
Quiz
Question comes here
Frequently Asked Questions
Yes, the area of a regular pentagon can be found using the formula A=¼*n*s^2*cot(π/n), whereas the area of an irregular pentagon can be found by breaking it down into simpler shapes.
Irregular pentagons can be divided into triangles, trapezoids or other simpler shapes to calculate their areas and sum it all up to find the total area of the pentagon.
A rectangular pentagon is an integer-sided convex pentagon with two non-adjacent sides that have identical lengths and form a right angle with the intervening side. Its area can be calculated as A = AT + Bd = PT + 2d = P (where AT and PT are the triangular portion’s integer area and perimeter).
Some of the real-world applications of pentagon area calculations are determining usable spaces in irregularly shaped plots of land, calculating areas of particular regions in maps, designing architectural elements, etc.
A pentagon’s area is calculated for solving a variety of practical problems like calculating the area of a pentagonal garden plot with different side lengths and interior angles for landscaping purposes.