Mastering the Area of Shapes: Formulas and Calculations for Various Geometric Figures
Comprehensive Definition, Description, Examples & Rules
Area in geometry is the total space a 2D shape or object takes. It has an important role in modern mathematics. It helps to define linear algebra and an important property of surfaces in differential geometry.
The area is calculated differently for all the shapes. The area calculation is different for all forms and is very simple for all. All shapes consist of a different formula for calculating the area of shapes.
In day-to-day life, determining the area of different shapes is very important. For example:
- Construction
- Interior Designing
These are real-life examples where you need to calculate the area of shapes.
Understanding Common Shapes and their Area Formula
Area formula for all shapes are different, and each has an area formula. These are:
Square: side × side
The formula of a square is a². A square consists of 4 equal sides, you multiply the length and the width to get your area.
Rectangle: length × width
For the area of a rectangle, you multiply the length by width, as the corresponding sides of the rectangle are equal.
Triangle: ½ × base × height
This is how you derive the formula for the common shapes.
Area of Circles and Circular Figures
Calculating the area of a circle is different. It is:
- Πr²
You multiply the pi with the square of the radius.
The components of the circle are:
- Radius: It is the distance from the outside edge of the circle to the center point of the circle. It is the primary component of a circle that helps in calculation.
- Diameter: A parallel line runs from one side of the circle to the other, passing through the center point.
A sector is part of a circle you can meet after creating an arc and its two radii. The area of a sector is:
- ∅/360° (πr²)
Here, r is the radius and ∅ is the angle of the sector.
An annuli is a particular area between two concentric circles. Concentric circles are the type that has a similar center and is in the same line. The area of an annulus is:
- π (R² – r²)
- π (R + r) (R – r)
Practical examples of circular shapes are:
- Coins
- Clock
- Dishes
- Wheels
- Dart Board
Calculating the Area of Irregular Shapes
To find the area of an irregular shape, you need to break the shape into a standard shape. The techniques are:
- Decomposition: It is the method in which you decompose and separate the irregular shape into two or more divisions to find its area. You calculate and add all the parts to get the total amount.
- Approximation: It is the method in which you approximately divide the irregular shape into unit squares, then calculate its area and add up the total amount.
The step-by-step examples for you are:
- Identify the irregular shapes.
- Divide the shape into regular shapes example (circle, half-circle, triangle, rectangle, and half-triangle)
- Calculate the area of all these regular shapes.
- Add the amounts to get the total figure.
A polygon can be termed an irregular shape, and to calculate the area, you use the shoelace formula or the shoelace method. You determine the area of a simple polygon with the formula:
Let the polygon plane be (x0,y0),…,(xn−1,yn−1 ). Then the area of the polygon may be calculated as:
- 1 2 (x0y1 − x1y0 + … + xn−2 yn−1 − xn−1 yn−2 + xn−1 y0 − x0yn−1 ).
Area of Polygons and Special Shapes
There are various formulas for the area of shapes you must follow, and the special shapes consist of different formulas. The area of different polygons are:
- Pentagon: ½ × perimeter × apothem
- Hexagon:{3 √3)/2}×a² (Here, ‘a’ represents the side of the hexagon)
- Octagon: 2(1+ √2) a² (Here, ‘a’ is a side of the octagon)
Calculating the area of special shapes:
- Parallelogram: base × height
It is a formula that you use to calculate the area of a parallelogram, similar to a square or rectangle formula.
- Trapezoids: ½ ( side + width ) height
- Rhombus: ½ × d1 × d2
These are the formulas for you to use for the shapes.
An Ellipse is a special circle stretched in a particular direction to give it an oval shape. The area of the shape is:
- Ellipse: πab
Here, ‘b’ is the length of the semi-minor axis, and ‘a’ is the semi-major axis length.
Finding Area using Coordinate Geometry
Coordinate geometry is used to calculate the dividing line ratio and will help find the line’s midpoint. You can calculate the area of shapes through the coordinate geometry by naming the vertices of the figure in a clockwise sequence or an anti-clockwise sequence. One of the primary examples of coordinate geometry is the shoelace formula.
The shoelace formula is a formula that can find out the area of a simple polygon using its vertices.
An example of practical exercises to follow for finding through coordinates is to use the X and the Y coordinates in a clockwise or an anti-clockwise sequence.
Area of 3D Shapes with Surface Area Vs. Volume
For the 3D shape, you calculate the volume of the shape. The surface area is how much space the object occupies, while the volume is the amount of space available inside the object.
Calculating the surface area of different shapes:
- Cubes: 6a² (a is an edge)
- Cylinders: 2πrh + 2π r² (r is the radius while h is the height)
- Spheres: 4 πr² (r is the radius)
Examples of real-life objects where you need to calculate a surface area are:
- Swimming pool
- Gas Cylinder
- Basketball (Sphere shaped)
Composite Figures and Compound Shapes
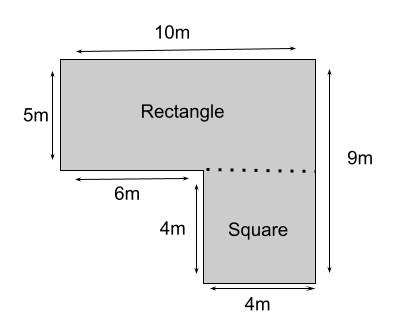
To find out the area of a composite or a compound shape, you must divide that shape into regular shapes and find the area of all the shapes and the total amount. The technique is similar to what you do for an irregular shape.
Practice Problems:
Area of composite shape = Area of rectangle + Area of square
I,e 50 + 16 = 66
Real-life examples of composite figures:
- House
- Cone
- Computer Mouse
Area in Practical Application
Calculating area is crucial in architecture and construction as it helps determine the dimensions of exterior walls and create accurate blueprints. Engineers need to calculate the height, length, and correct area measurements before commencing house construction.
Calculating area is critical for various purposes, including land measurement and agriculture. It plays a crucial role in determining crop production and is also used to calculate taxes based on land size.
The area connects with design and art, as drawing and designing often involve precise calculations of specific measurements.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Calculating the area of shapes is a vital part of geometry and mathematics.
- Different shapes have different formulas for calculating their area and perimeter.
- You need to break down the irregular shapes into regular shapes to calculate the area.
- Calculating the area is part of the day-to-day human life in architecture, art, and design.
Quiz
Question comes here
Frequently Asked Questions
The formula is:
- ½ ( side + width ) height.
It is a complex shape, and you can use this formula to calculate your desired amount.
Finding the area of a polygon with the given side lengths will be a regular polygon and won’t use the shoelace formula. The formula to use is:
- (n/2) × L × R
N = Number of sides
L = Length of a side
R = Radius of an inscribed circle.
The process for finding the area of irregular shapes is to subdivide it into regular shapes and calculate the area of all these shapes. Finally, add all the amounts to get the result of the total amount.
The formula to use for calculating the area of an ellipse is:
- Πab
Here, ‘b’ is the length of the semi-minor axis, and ‘a’ is the semi-major axis length.
The real-world applications where you calculate the area of something are:
- Carpets
- Floor-covering
- Cupboards
- House Designing
- Gas Cylinder
You need to use a similar technique for the irregular shapes by subdividing the compound shape into a regular shape and calculating each area.