Mastering Congruent Triangles: Your Guide to Geometry Excellence
Comprehensive Definition, Description, Examples & Rules
Introduction to Congruent Triangles:
The congruent triangle is a significant concept in math. Two triangles of similar shape and size are referred to as congruent. This page will provide an overview of the congruent triangle concept, its significance, and its formulas. At the end of this page, you will find a worksheet that will help you analyze your understanding of this concept.
Congruent triangles and their significance.
When two triangles have a similar shape and size, we can consider them congruent. Congruent triangles are significant in geometry due to various reasons:
- It becomes easy to solve the equation. If you have clarity related to the congruent triangle, You can use congruent triangle properties and get the solution.
- The congruent definition triangles are also relevant in construction. It is helpful in building accurate structures.
Understanding Congruence of triangle
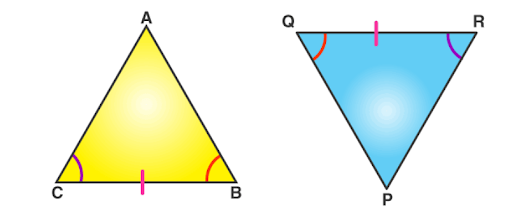
congruent triangles meaning is equal size and shape of a geometric figure. Similar size and shape mean similar angles between two shapes.
Concept of congruence in geometry and similar triangles.
- There is a similar size and shape of a geometric figure in the congruent concept.
- On the other hand, similar figures don’t have similar sides. It may have a similar shape, but there is a difference in the angles of both shapes.
- Congruence has the symbol ≅, and similar figures have the symbol ∼.
real-world examples illustrating congruent objects.
The congruence of triangles is a significant concept in daily life. Anything of similar size and shape can be considered congruent, like:
- Two earthen poets with equal dimensions and similar shapes and sizes are congruent.
- Square-shaped tiles with equal dimensions can be considered congruent.
- A4-size sheets that are the same size and shape are also congruent.
Congruence criteria for triangle:
You will find a variety of criteria for triangle congruence in the section.
Fundamental criteria for proving triangle congruence:
Here are the basic congruence rule to be followed:
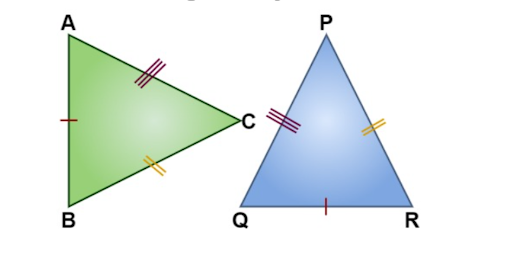
1. Side-Side-Side (SSS)
The SSS types criteria are used for proving congruence in two triangles. In this criterion, you are expected to prove all three sides are equal to each other.
For example:
If you want to prove congruence between two triangles, ABC and XYZ, with the side-by-side method, then you have to follow some steps:
- You have to measure the length of both triangles separately, like AB, BC, and AC, and XY, YZ, and ZX.
- If you find AB=XY, BC=YZ, and AC=ZX, then you have proven the congruent triangle with the side-by-side method.
2. Side-Angle-Side (SAS)
Side angle side is a different criterion for finding a congruent triangle. In this criterion, you need to prove two sides and angles similar to other triangle sides and angles.
For example:
If you want to prove the congruence of two triangles, ABC and XYZ, with the side-angle-side method, then
- You have to measure the length of both triangles separately, like AB, BC, and AC, and XY, YZ, and ZX.
- You also need to measure the angle between triangles XYZ and PQR.
- If you find AB=XY, BC=YZ, and the angles of both triangles equal to each other, then you have proven a congruent triangle with SAS.
3. Angle-Side-Angle (ASA)
In this criterion, you need to prove one side and two angles are equal to each other.
For example:
If you want to prove the congruence of two triangles, ABC and XYZ, with the angle-side-angle method, then:
- In the first step, you need to measure the two angles of both triangles. Like the ABC triangle (angle A and angle B) and the PQR triangle (angle P and angle Q),
- You also need to measure one side of both triangles, like in ABC triangle AB and in XYZ triangle XY.
- If you find angles A and B equal to angles P and Q, then you have proven the congruence of these two triangles through ASA.
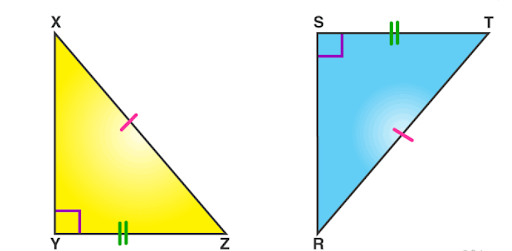
4. Hypotenuse-Leg (HL)
This criterion is used for proving congruence in a right-angled triangle. In this criterion, you have to prove one hypotenuse and one leg of the right-angle triangle are equal to the other triangle hypotenuse and leg.
For example:
If you want to prove congruence in two right-angled triangles, ABC and XYZ, with HL criteria, then:
- You need to measure the length of the hypotenuse of both right-angled triangles. Like in ABC (measure length of AC) and in XYZ (measure length of ZX),
- Then, you need to measure the legs of both right-angled triangles; for example, like in ABC, it is BC, and in XYZ, it is YZ.
- If you find a hypotenuse that is AC equal to ZX and a leg that is BC equal to YZ, then you have proven the congruence of two triangles with the HL method.
The Congruence Symbol (≅):
Congruence symbol and its usage in geometry.
The symbol ≅ represents the equal sides and shapes of two geometric figures. You can represent the congruent triangle using this symbol if two triangles have the same shape, size, or angles.
For example:
- You can represent the triangle ABC and XYZ as equal to each other by proving its sides, like AB, BC, and AC, and XY, YZ, and ZX, as equal to each other.
- Once you find the sides and angles equal, you can represent it as
- Triangle ABC ≅ XYZ.
Proving Congruence:
You can prove congruence with a specific method. It involves various steps that you need to follow to prove congruence.
There are various steps that you need to follow to prove:
- You need to mention the term ‘given’ for the information related to the statement. It may contain information related to the type of triangle, sides, and angles.
- Then, you need to choose the congruence triangle criteria as per the given condition.
- Once you apply the criteria, you need to give reasoning.
- After following these steps, find two congruent triangles. You have to use the term ‘Hence proved’.
- For example:
- Hence proved, ABC ≅ XYZ.
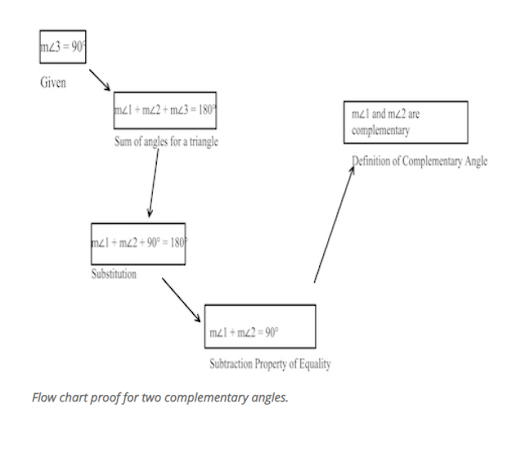
The flowchart to simplify this process is:
Here you can see the given statement and conclusion after using logical reasoning.
The importance of proper reasoning and logical steps
- Logical reasoning is significant in providing the information that you have using an accurate method of logic.
- If you use logical steps and provide reasoning, then you will get the right answer.
Congruent Triangles in Real Life:
The congruent triangle is a real-life concept. It deals with various sectors like engineering, construction, architecture, and so on. You will find its usage at a practical level in this section.
Practical applications of congruent triangles in everyday scenarios.
- In architecture, congruent triangle coordinates are used for developing a design. An architect may use a congruent triangle to make an accurate design.
- In engineering, this concept is used for constructing roads. The congruent concept provides an accurate idea of the sides and angles.
- In construction, a congruent triangle is used to give shape to your house. A congruent concept is used for adjusting the furniture. If you have a triangular space and you want a frame to be placed in that space, then it can be easily fit because the triangle space and frame are the same size and have the same sides.
- In mathematics, the concept of a congruent triangle is used to prove the similarity of the shape and size of two triangles.
- The congruent concept is used in navigation and other domains.
Congruence in Different Types of Triangles:
Congruence can be proven in different types of triangles. Its criteria may be different from one another.
Congruence application to various types of triangles (e.g., right triangles, equilateral triangles, and isosceles triangles).
Congruence applies to various types of triangles, like:
- Right angle: The right angle triangle has a 90° angle on one side. In a right-angle triangle, you need to use HL criteria. In HL criteria, you need to prove one hypotenuse side and one leg side of a right-angle triangle are equal to the other right-angle triangle hypotenuse and leg side.
- Equilateral triangle: An equilateral triangle has the property that all three sides are equal to each other. It is 60⁰. Although equilateral, all sides are equal to each other, so it is automatically a congruent triangle.
- Isosceles triangle: It has equal sides of two triangles with opposite angles. You can use side-angle-side congruent criteria to prove two isosceles triangles are congruent.
Common Misconceptions and Pitfalls:
There are various misconceptions about the congruent triangle among the students.
- Students get confused with the congruence criteria.
- Students didn’t observe the types of triangles. That’s impacting the results.
- In general, students mistakenly use angles rather than sides.
- They forgot the congruent triangle symbol to be used.
- Sometimes, they prefer angles over sides.
Tips for avoiding these pitfalls.
These are the various tips through which students can avoid such pitfalls:
- It is necessary for students to use congruent triangles.
- They should be clear from both angles and sides.
- Students should remember the congruence criteria and their usage.
Interactive Quizzes and Exercises:
Here is the quiz that will check your practical understanding of this concept.
What is a congruent triangle?
- A congruent triangle is a similar-shaped triangle.
- When two triangles have similar shapes, we refer to them as congruent triangles.
- Two triangles with similar shapes and sides are known as congruent triangles.
- None of the above
What is the symbol of a congruent triangle?
- ≅
- –
- +
- †
What kind of criteria is expected to be used in a right-angled triangle?
- S-S-S
- S-A-S
- HL
- ASA
The correct answer for the given quiz is:
- C
- A
- C
- If you get all the answers correct, then you need more practice to solve advanced questions.
- If you didn’t get a good score on this quiz, then you need to revise the concept and solve the questions logically.
Infographic:
These are the Garu infographics that can provide you with better clarity.
Side-Side-Side (SSS)
Side-Angle-Side
Angle-Side-Angle
Hypotenuse-Leg
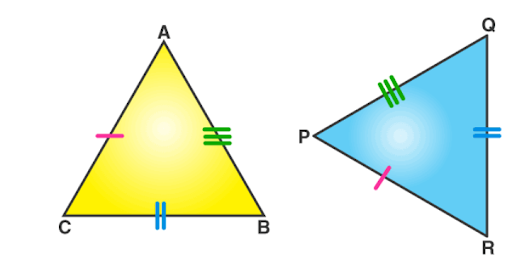
In this infographic, you can observe the two triangles with equal sides and sizes.
A flowchart showing the step-by-step process of proving triangle congruence.
This is the flow chart that gives insights into the congruent triangle properties.
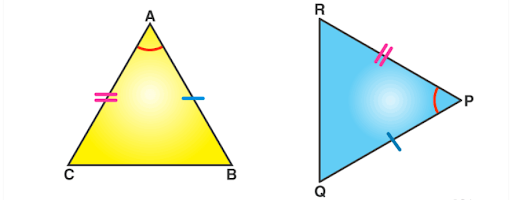
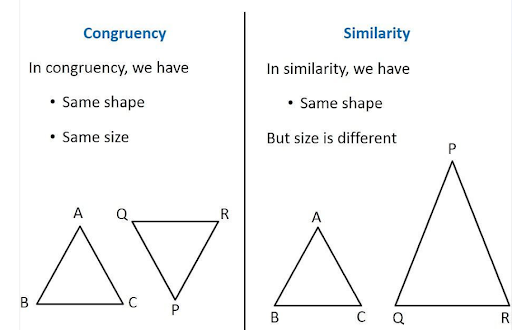
Comparing congruent and similar triangles.
A congruent triangle has a similar size and shape, whereas a similar triangle has a similar shape but no similar sides. It can become clear with the graphic.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Two triangles of similar shape and size are referred to as congruent. Congruence refers to the size and shape of a geometric figure.
- This concept is different from a similar triangle concept. Congruence has the symbol ≅, and similar figures have the symbol ∼.
- A congruent triangle has a similar size and shape, whereas a similar triangle has a similar shape but no similar sides.
- This concept can be used for equilateral, isosceles and right-angle triangles.
- There are various misconceptions among the students related to the congruent triangle and its criteria.
- There are four criteria of a congruent triangle that is Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA) and Hypotenuse-Leg (HL).
- Students can develop practical understanding through practice on worksheets related to congruent triangles.
Quiz
Question comes here
Frequently Asked Questions
You can determine two triangles as congruent by their similar sides and angles.
This ≅ is the congruent symbol, and it is used to represent that two triangles are congruent. For example, ABC ≅ XYZ.
Side-by-side is the most commonly used congruence criterion for triangles.
A congruent triangle has a similar size and shape, whereas a similar triangle has a similar shape but no similar sides.