Exploring Parallelograms
Comprehensive Definition, Description, Examples & Rules
Introduction to Parallelograms
A parallelogram, a fundamental 2D geometric shape, boasts two sets of parallel sides with equal lengths. Within this class of quadrilaterals, adjacent angles consistently sum up to 180 degrees, imparting a significant attribute to its structure. In geometry, there are a myriad of 2-D shapes and figures, ranging from squares and rectangles to circles and rhombuses, each uniquely defined by their distinct characteristics. Hence, for a complete understanding of the parallelogram, it is needed to explore its parallelogram definition and parallelogram meaning, characteristics, significances, and properties.
Parallelogram Definition
A parallelogram is defined as a two-dimensional geometric shape and possesses two sets of parallel sides with equal lengths.
What is a Parallelogram Shape?
A quadrilateral, or four-sided polygon, is one kind of parallelogram. However, not all quadrilaterals are parallelograms. A quadrilateral may or may not have parallel sides, whereas a parallelogram has two pairs of parallel sides. This is the primary difference that makes parallelograms special. Stated otherwise, a parallelogram is a unique kind of quadrilateral consisting of two sets of parallel sides.
Parallelogram Properties
A quadrilateral is referred to as a parallelogram if it possesses two opposed and parallel sides. The following are a parallelogram’s characteristics:
- The opposing sides are equal and parallel.
- Equal opposite angles are a must.
- The angles adjacent/next to each other are supplementary.
- Every other angle will be at a right angle if there is one that is a right angle.
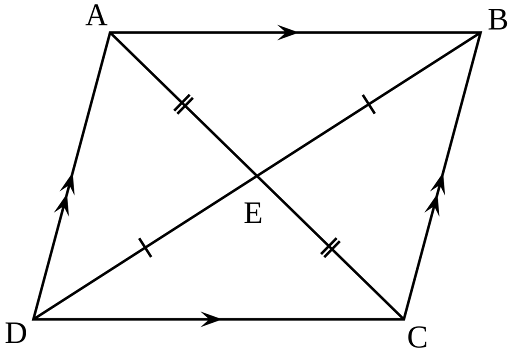
- The two diagonals bisect each other.
- A parallelogram is divided into two congruent/equal triangles by each diagonal.
- A parallelogram’s sum of the squares for each of its sides equals the sum of the squares for each of its diagonals. Another name for it is parallelogram law.
Types of Parallelograms
Square and Rectangle: Two shapes that resemble parallelograms are the square and the rectangle. Each has an equal and parallel opposing side to the other. Both shapes’ diagonals cut each other in half.
Rhombus: When all sides are equal in a parallelogram, it is called a rhombus.
Rhomboid: The parallelogram in which the neighboring sides have different lengths but the opposing sides are parallel to one another. The angles are not straight either.
Trapezium: A quadrilateral with only one pair of parallel sides is called a trapezium. The other two sides are referred to as “legs” or lateral sides, while the parallel sides are termed “bases.”
Real-Life Parallelogram Examples
Here are a few instances of parallelogram shapes in real life:
- The solar panel is a popular renewable energy source that is often built in the form of a parallelogram or rectangle. These solar panel shapes are the most popular since they are easiest to install on the roof terrace.
- The staircase’s common structure has a parallelogram form as well.
- Rectangular furniture is used in our daily work; examples include the desk we use for work or study, the dinner table, the dressing table, and other similar pieces.
- Different shapes and sizes of tiles are available for covering the ground, floors, and other surfaces. The square, rectangle, rhombus, and parallelogram are a few of the common shapes.
- From the side, the parallelogram-shaped roof of a cottage is reminiscent of a saltbox, shed, or gable roof.
- In addition to the given examples, modern constructions also employ other parallelogram patterns to produce distinctive architectural designs. In addition, kid’s stationery items, such as rulers, sharpeners, and erasers have a parallelogram form.
Infographic: "Parallelograms in Action"
Visual Representation of Parallelogram Examples
Exploring Rectangles and Squares
Square
A parallelogram with four equal sides and angles is called a square. Because its sides and angles are equal, it is also a regular quadrilateral. A square has four right(90°) angles, the same as a rectangle does. Another way to visualize it is as an equal-sided rectangle with two neighboring sides.
The following three characteristics of a square are:
- A square’s angles are all 90 degrees.
- A square has equal and parallel sides on all sides.
- Perpendicular diagonals split each other in half.
Square formula: the perimeter and area of a square
Let ‘s’ be the side of a square, so:
- Square footage = s × s = s²
- Square perimeter = 2 × (s + s) = 4s
Rectangle
A rectangle has identical angles all around (360°/4 = 90°). In addition, diagonals divide a rectangle’s opposite sides, which are parallel and equal.
Features of a Rectangle
- The three characteristics of a rectangle are as follows:
- A rectangle has 90° angles at every point.
- A rectangle’s opposite sides are equal and A rectangle’s parallel diagonals split across one another.
Rectangle formula: the rectangle’s area and perimeter
When the rectangle’s length is L and its width is B, then,
Length × Breadth, or L × B, is the area of a rectangle.
Rectangle perimeter = 2 × (L + B)
Parallelogram vs. Rhombus
Parallelogram | Rhombus |
A parallelogram is a two-dimensional figure consisting of only equal opposing sides. | A two-dimensional figure with parallel sides on all four sides is called a rhombus. |
The formula area=b*h can be used to find a parallelogram’s area. Where the parallelogram has a height of h and a base of b. | The formula Area = d1, d2/2 can be used to find the area of a rhombus. The symbols d1 and d2 stand for a rhombus’s diagonals. |
All that is equal are the lengths of the opposing sides. | All of the four sides have equal length. |
When the diagonals of a parallelogram cross, congruent triangles result. | When the diagonals of a rhombus meet at a right angle, a scalene triangle is created. |
Not all parallelograms are rhombuses. | All Rhombus is a Parallelogram |
Parallelogram vs. Trapezoid
Parallelogram | Trapezium (Trapezoid) |
A quadrilateral with opposing sides that are parallel and of equal length is called a parallelogram. Moreover, the opposing angles are equal. | A quadrilateral with one pair of parallel sides and one pair of non-parallel sides is called a trapezium. |
Parallelograms come in a variety of shapes, such as squares, rhombuses, rectangles, and others. | There are several variations of trapeziums, including variations in side lengths and angles. |
The lengths of the two pairs of opposing sides are equal and parallel. | There is only one parallel pair of opposing sides. |
The measure of opposite angles is equal. | The non-parallel angles sum up to 180 degrees, despite the angles’ different measures. |
A parallelogram’s diagonals connect at their midpoints because they are bisecting one another. | A trapezium’s diagonals do not always intersect each other. |
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Parallelogram is an important two-dimensional shape with some specific properties.
- There are different parallelograms definitions or parallelograms meaning, but the characteristics remain constant.
- Parallelograms have many practical uses in everyday life.
- The area and perimeter of a parallelogram can be calculated using its base, height, and side lengths.
- Understanding the characteristics of a parallelogram, such as opposite sides being parallel and opposite angles being congruent, is essential in geometry.
Quiz
Question comes here
Frequently Asked Questions
To check if a shape is a parallelogram, focus on its sides and angles. Look for opposite sides that run in the same direction and are the same length. Also, make sure that opposite angles match in size. If you find these characteristics in the shape, it’s a parallelogram.
To calculate the area of a parallelogram, use this simple formula: area = base × height. Picture the shape as a rectangle with a tilted top. The base is the length of one of the shorter sides, and the height is the perpendicular distance between the two bases. Multiply these values, and you’ve got the area
The diagonals of a parallelogram are like invisible lines connecting opposite corners. What’s unique is that they meet at the center, dividing each other into equal parts.
Yes, a square can be considered a parallelogram. In fact, it’s a special kind of parallelogram with all the typical parallelogram characteristics. It has twin sides and angles just like any other parallelogram but with an extra feature: all four corners have right angles, making it a unique type of parallelogram.