Unlocking Quadrilateral Areas: Formulas, Insights, and Applications
Comprehensive Definition, Description, Examples & Rules
Introduction to Quadrilaterals
A polygon with a total of four edges and sides is referred to as a quadrilateral. Quadrilaterals come in a variety of shapes like squares, rectangles, parallelograms, and trapeziums. Each of these different kinds of quadrilaterals has unique properties that are specific to them. Quadrilaterals have an important role to play in geometry as they help us to do constructions, and calculate the area and perimeter of various kinds of shapes. They also have an essential role to play in various real-life applications like architecture, engineering, and more.
Understanding Quadrilaterals
We call those polygons quadrilaterals that have four sides and four vertices. Quadrilaterals show various properties that are unique to them, for example:
- All quadrilaterals have four sides.
- All internal angles in a quadrilateral sum up to 360 degrees.
- All external angles in a quadrilateral sum up to 360 degrees.
- A quadrilateral can have up to two diagonals or line segments connecting opposite vertices.
The Quadrilateral Area Formula
The area formula for quadrilaterals can be defined as:
A= 0.5 * d1 * d2 SIN (θ)
Here is a detailed explanation of all the components used in the formula:
- A: Area of the quadrilateral
- d1 and d2: The lengths of the two diagonals of the quadrilateral.
- Θ: The angle that lies between the two diagonals.
Finding the Area of a Quadrilateral
Here is a step-by-step procedure for computing the area of a quadrilateral using the formula given above:
Step 1
Identify the diagonals in the given quadrilateral and the included angle(θ).
Step 2
Put the values for diagonal 1 and 2, and θ in the formula to compute the total area of the quadrilateral.
Here are some numerical examples to help you understand the area calculations better:
Example 1
Find the area of a quadrilateral with diagonals of length 10 cm and 8 cm and θ as 45 degrees.
Solution
We know that the quadrilateral formula for area is: A = 0.5 * d1 * d2 * sin(θ)
After putting in the values,
A= 0.5 * 10 * 8 * 0.7071 [sin(45)= 0.7071]
Hence, A= 30.84 cm^2
Example 2
Find the length of one of the diagonals of a quadrilateral with the other diagonal of length 10 cm, area as 50 cm^2, and θ as 90 degrees.
Solution
We know that the quadrilateral formula for area is: A = 0.5 * d1 * d2 * sin(θ)
After putting in the values,
50= 0.5 * 10 * d2 * 1 [sin(θ)= 1]
Transposing the values,
50= 50 * d2
d2= 1
Hence, the length of the other diagonal is 1 cm.
Infographics: Visual Representation
Here is a visual representation to demonstrate the formula and the concept of quadrilateral area:
Rectangle
Square
Parallelogram
Trapezoid
Special Types of Quadrilaterals
There are a variety of quadrilaterals and each one of them has their unique properties and different formulas for calculating their area. Here is a list of different types of quadrilaterals and their specific area calculation formula:
Rectangle
We call those quadrilaterals rectangles that have four right angles, four sides and also have two opposite pairs of sides equal in length. The area of a rectangle is calculated using the given formula:
A= l * b
Where,
‘A’: area of the rectangle.
‘l’: length of one of the sides of the rectangle.
‘b’ refers to the breadth of one of the sides of the rectangle.
Square
We call those quadrilateral squares that have four right angles, four sides and all four sides equal in length. The area of a square is calculated using the given formula:
A= s^2
Where,
‘A’: the area of the rectangle.
‘s’: the length of any one of the sides of the square.
Parallelogram
A quadrilateral having opposite sides as equal in length and parallel to each other is called a parallelogram. A parallelogram’s area can be computed using the formula:
A= b * h
Where,
‘A’: the area of the rectangle.
‘h’ refers to the height of the parallelogram.
‘b’ refers to the measure of the base of the parallelogram.
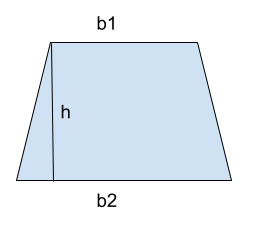
Trapezoid
A trapezoid is a quadrilateral that has at least one pair of sides that are parallel to each other, known as the bases. The area of a trapezoid can be computed using the given formula:
A= b1 + b2 / 2 * h
Where,
‘A’: the area of the rectangle.
‘b1’ and ‘b2’ refer to the length of the bases or the two equal sides.
‘h’ refers to the height of the trapezoid or the perpendicular distance between the bases.
Real-World Applications
Quadrilaterals are used in a variety of real-world applications like:
Land Surveying: Quadrilaterals can be used to calculate the area of plots of land and determine the right market prices for them.
Architecture: Quadrilaterals can be used to design creative floors for houses in various shapes, determine the quantity of materials needed for the project, etc.
Construction: Quadrilaterals can be used to determine the area upon which a building or a structure would be founded to ensure precise distribution of the total load, which is very crucial in construction.
Comparing Quadrilaterals with Other Shapes
Different types of shapes have different formulas for calculating their area. Here is a representation of the different formulas used for different kinds of shapes:
Quadrilaterals
The quadrilateral area formula is given as: A = 0.5 * d1 * d2 * sin(θ)
Where,
- A: Area of the quadrilateral
- d1 and d2: The lengths of the two diagonals of the quadrilateral.
- θ: The angle between the two diagonals.
Triangles
The formula for calculating the area of triangles is given as A= ½ * b * h
Where,
- A: Area of the triangle
- b: Base of the triangle
- h: Height of the triangle
Circles
The formula for calculating the area of circles is given as A= πr^2
Where ‘r’ stands for the radius of the circle.
Common Mistakes and Pitfalls
Here is a list of some common errors that people make while calculating the area of quadrilaterals and how to avoid them:
- Using the wrong formula: Always remember that every quadrilateral has its formula for calculating its area. You should keep yourself abreast of all the specific formulas for calculating the area for different quadrilaterals to make accurate calculations.
- Using different units: make sure that you use the same kind of units throughout the formula to avoid any discrepancies in the final result.
- Inaccurate measurements: Make sure to take the correct measurements of sides and angles to calculate the area of quadrilaterals precisely.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Any four-sided polygon in geometry is known as a quadrilateral.
- Quadrilaterals come in a variety of shapes like squares, rectangles, parallelograms, and trapeziums.
- Quadrilaterals are used in various real-life processes like architecture, construction, engineering, etc.
Quiz
Question comes here
Frequently Asked Questions
The formula for calculating the area of a quadrilateral is 0.5 * d1 * d2 * sin(θ), while that of triangles is ½ * b * h, and of circles is πr^2.
Here are specific area formulas for different kinds of quadrilaterals:
Rectangle: l*b
Square: s^2
Parallelogram: b * h
Trapezoid: b1 + b2 / 2 * h
In architecture, quadrilaterals are used to design floors and in construction, they are used to determine the area of foundation for various kinds of structures.
Some common mistakes to avoid when calculating the area of a quadrilateral are using the wrong formula for quadrilaterals and different units in the formula. Some strategies that can ensure accurate results are knowing the correct area formula for each quadrilateral and maintaining the same units for calculation throughout the formula.
Yes, different types of quadrilaterals have unique characteristics or properties that affect their area calculations. For example, a square has all sides equal in length, a rectangle has two different pairs of equal sides, etc. These properties have a crucial role to play in determining the area of various quadrilaterals.