Understanding Types of Angles: A Comprehensive Guide
Comprehensive Definition, Description, Examples & Rules
What are the types of angles, angle names, and the difference between obtuse and acute???? Are these questions troubling you? Well, then let Edulyte put your worries to rest. With these resources, you get exclusive tricks to understand angles and learn to handle angle calculations easily!
Introduction: Angles In Our Daily Lives
Did you know that the importance of understanding types of angles in geometry extends far beyond the classroom?
- Angles in geometry provide a framework for measuring and describing the orientation of lines and shapes, enabling mathematicians to analyse and solve complex problems related to space and dimension.
- In physics, angles are integral to the study of motion, forces, and equilibrium. Concepts such as projectile motion, vectors, and the principles of mechanics heavily rely on an understanding of angles.
- In engineering, different types of angles are essential in the design and construction of structures. Civil engineers, architects, and mechanical engineers, among others, use angles to ensure the integrity and functionality of their designs.
Fundamentals of Angles: Definition And Angles Names
Definition of Angles
In geometry, an angle forms when two rays or line segments share a common endpoint called the vertex. The rays extending from the vertex are the sides of the angle. Angles are measured in degrees.
Significance of Angles
The significance of types of angles extends from mathematics to physics, engineering, navigation, and various other disciplines where spatial relationships play a vital role.
Basic Classification of Types of Angles Based on Measurement
Acute Angle:
- It measures less than 90 degrees.
- Example: A 45-degree angle is acute because it is less than 90 degrees.
Obtuse Angle:
- It measures more than 90 degrees but less than 180 degrees.
- Example: A 120-degree angle is obtuse, greater than 90 degrees but less than 180 degrees.
Right Angle:
- A right angle is exactly 90 degrees.
- Example: The angle formed by the meeting of the adjacent sides of a square is a right angle.
Straight Angle:
- A straight angle is exactly 180 degrees.
- It forms a straight line, and the two rays or line segments constituting it are opposite and collinear.
- Example: The angle formed by a straight line is straight.
Searching for the ideal Maths assistance catering exclusively to your study needs? Sign up for free. Check out our tutors and get classes customised to your specific learning needs!
Common Angle Names
All types of angles are classified based on their measurements and characteristics. Here are some commonly used angle names:
Acute Angle:
- It measures less than 90 degrees.
- Examples: 30 degrees, 45 degrees, and 60 degrees are all acute angles.
Obtuse Angle:
- It measures more than 90 degrees but less than 180 degrees.
- Examples: 100 degrees, 120 degrees, and 150 degrees are all obtuse angles.
Right Angle:
- A right angle is exactly 90 degrees.
- It forms a perfect “L” shape.
- Example: The angle formed by the corner of a square is a right angle.
Straight Angle:
- A straight angle is exactly 180 degrees.
- It forms a straight line, and the two rays or line segments constituting it are opposite and collinear.
- Example: The angle formed by a straight line is straight.
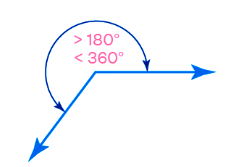
Reflex Angle:
- It measures more than 180 degrees but less than 360 degrees.
- It is formed by continuing one of the angle’s sides beyond 180 degrees.
- Example: An angle measuring 220 degrees is a reflex angle.
Check out free Maths resources and worksheets to brush up your calculation skills.
Types of Angles Based on Measurement
Angles can be classified into various types based on their measurements. Understanding these types is crucial in geometry. Here’s a detailed exploration of different angle measurements, focusing on acute angles, obtuse angles, and right angles:
Acute Angle:
- It measures less than 90 degrees.
- Acute angles are characterised by their sharpness and are commonly found in triangles and other geometric shapes.
- Examples: A 30-degree angle, a 45-degree angle, and a 60-degree angle are all acute angles.
Obtuse Angle:
- It measures more than 90 degrees but less than 180 degrees.
- Obtuse angles are broader and less sharp than acute angles.
- Examples: A 100-degree angle, a 120-degree angle, and a 150-degree angle are all obtuse angles.
Right Angle:
- A right angle is exactly 90 degrees.
- It forms a perfect “L” shape, resembling the corner of a square or rectangle.
- Right angles are crucial in geometric constructions and are often used as a reference point for measuring and constructing other angles.
- Example: The angle formed by the intersection of two perpendicular lines is right.
Special Types of Angles
In addition to the primary classification of angles based on measurement, there are special types of angles that exhibit specific relationships with one another.
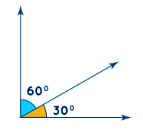
Complementary Angles:
- Sum of complementary angles is precisely 90 degrees.
- In other words, when you add the measure of one angle to the measure of another angle, the result is a right angle (90 degrees).
- Example: If one angle measures 45 degrees, its complementary angle would measure 45 degrees as well (45 degrees + 45 degrees = 90 degrees).
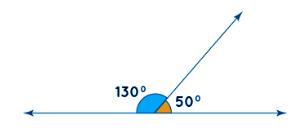
Supplementary Angles:
- Two angles are supplementary when their sum is exactly 180 degrees.
- Adding the measure of one angle to the measure of another angle results in a straight line.
- Example: If one angle measures 120 degrees, its supplementary angle would measure 60 degrees (120 degrees + 60 degrees = 180 degrees).
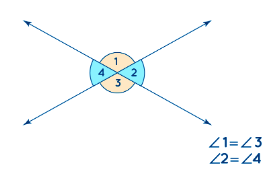
Vertical Angles:
- Vertical angles are pairs of angles formed by intersecting lines. They are opposite each other and share a common vertex.
- Vertical angles are always congruent, meaning they have the same measure.
- Example: If ∠A and ∠B are vertical angles in the intersecting lines, then ∠A = ∠B.
Polygons and Angles
Polygons are closed geometric figures with straight sides. The angles within polygons define their properties and characteristics.
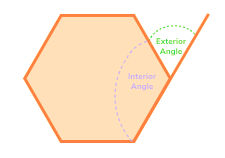
Interior Angles of a Polygon
- Sum of interior angles of polygon = (where n is the number of sides) 180∘×(n−2).
- In a regular polygon (a polygon with all sides and angles equal), every interior angle is the result of dividing the sum of the interior angles by the number of sides.
Example:
- In a triangle (n=3), the sum of interior angles is 180∘×(3−2)=180∘. Therefore, each interior angle in a triangle is 180∘/3=60∘.
Exterior Angles of a Polygon
- An exterior angle of polygon is formed between one side of the polygon and the extension of an adjacent side.
- Sum of exterior angles of polygon, regardless of the number of sides, is always 360∘.
Example:
- In a triangle, each exterior angle is supplementary to its corresponding interior angle. If one interior angle is 60∘, the corresponding exterior angle is 180∘−60∘=120∘.
Applications of Angles
- Building Design and Construction: Architects use angles extensively in designing and constructing buildings. Right angles ensure structural stability, while acute and obtuse angles contribute to the aesthetics and functionality of architectural elements.
- Structural Engineering: = Understanding the angles formed by beams, trusses, and other components is essential for ensuring the structural integrity and stability of bridges, buildings, and other infrastructure.
- Mechanical Engineering: The angles of gears, cam profiles, and linkages are critical for achieving specific mechanical movements and functionalities.
- Navigation: In navigation, understanding angles is fundamental for determining direction. Nautical charts, maps, and GPS systems rely on angles to provide accurate information about routes and locations.
- Sports: In sports like golf, billiards, or archery, players consider the angles of impact or trajectory to achieve desired outcomes.
- Home Improvement: DIY projects and tasks like cutting mouldings involve angles. An understanding of angles is required for measuring and cutting materials and installing fixtures.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Understanding angles is foundational to geometry.
- Angles are classified based on their measurements, with acute angles (less than 90 degrees), obtuse angles (more than 90 degrees but less than 180 degrees), and right angles (exactly 90 degrees) being common types.
- Special types of angles, such as complementary angles (sum to 90 degrees), supplementary angles (sum to 180 degrees), and vertical angles (opposite angles formed by intersecting lines), have specific properties that aid in problem-solving
- The sum of interior angles in a polygon is determined by the formula 180∘×(n−2), where n is the number of sides.
- Angles have practical applications in various fields, including architecture, engineering, navigation, and daily activities.
Quiz
Question comes here
Frequently Asked Questions
- Two angles are complementary if they sum up to exactly 90 degrees.
- Two angles are supplementary if they add up to exactly 180 degrees.
Angles are closely related to polygons; understanding this relationship is fundamental in geometry. Here are some critical aspects of how angles relate to polygons:
Interior Angles: Sum of interior angles of polygon formula Sum=(n−2)×180∘ (n = number of sides).
Exterior Angles: An exterior angle of a polygon forms between one side of the polygon and the extension of an adjacent side. Sum of exterior angles of polygon is always 360∘
Vertical angles are pairs of angles formed by the intersection of two lines. They share a common vertex but are not adjacent angles; instead, they are opposite each other. Vertical angles are always congruent, meaning they have the same measure.
Some of the ways to determine the measurement of an angle are:
Protractor: The most direct method is to use a protractor. Place the protractor’s centre over the angle’s vertex, align one side of the angle with the baseline of the protractor, and read the measurement where the other side intersects the protractor scale.
Known Angle Relationships: If the angle is part of a geometric figure with known angle relationships (e.g., a triangle or a straight line), you can use those relationships to find the angle.
Complementary and Supplementary Angles: If you have information about complementary or supplementary angles, you can use that information to find the angle.
Trigonometry: If you have information about the sides of a right-angled triangle, you can use trigonometric functions (sine, cosine, tangent) to find the angle.