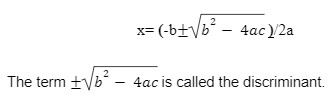Mastering Algebraic Equations: A Step-by-Step Guide to Solving Equations and Expressions
Comprehensive Definition, Description, Examples & Rules
Introduction to Equations and Algebraic Expressions
Algebraic equations use letters from the alphabet to denote numbers without actually putting a value to them.
We learn how to express an unknown value using letters like x, y, and z in the fundamentals of algebra. These letters are known as variables, as they get assigned different values depending on the equation. You will learn more about this as you keep reading.
Importance and relevance of algebraic equations in mathematics and real-life applications
Algebra equations might seem like something you study about and solve in a math textbook, but it has multiple uses in our real life as well.
- Algebraic expressions have helped us solve many complex mathematical problems throughout the ages. This has led to multiple discoveries and scientific breakthroughs.
- Algebraic equations are used in computer programming. A lot of web applications, softwares etc are dependent on the right formula and equation.
- Algebra equations are used in economics to calculate revenue, find out the cost, loss, profit and other similar things.
If you know how to solve algebra equation you are automatically better at solving quantitative and reasoning problems.
Understanding Algebraic Equations
Different types of algebraic equations (linear, quadratic, etc.)
Each variable has a specific degree assigned to it. That determines the type of algebraic equations that we are dealing with. The highest power of a variable in an algebraic equation is called its degree
Types of Polynomials Based on their Degrees
Degree | Type | Example |
|---|---|---|
Degree 0 | Constant Polynomial | x=4 |
Degree 1 | Linear Polynomial | 3x+4=0 |
Degree 2 | Quadratic Polynomial | 2x2+5x-9=0 |
Degree 3 | Cubic Polynomial | 6x3-4x2+7x-26=0 |
Components of an algebraic equation (variables, constants, coefficients)
Let’s understand this with an illustration. Take the equation 5x + 10 = 55 for example. In this
- x is a variable, it can take any value
- 5 is the coefficient of x, as it is a constant value which accompanies the variable.
- 10 is the constant. It has a definite value
Examples to illustrate various types of equations
The following are some of the basic topics.
Solving Linear Equations
Here are two methods for solving Linear equations
The Substitution method
Consider a system of equations with two linear algebraic equations with the variables x and y. The substitution method focuses on one equation and finds out the value of one variable in that equation in terms of the other variable. It then substitutes this value for the original variable in the other equation.
The Elimination method
The elimination method can be used to solve a system of equations containing two variables.. As the name suggests, the Elimination method depends upon adding or subtracting the system of equations until one variable is eliminated.
Consider the example:
-9y+4x=20
-7y+16x=80
Multiply the equations in so that both the coefficients of one of the variables become negative of each other. We will use -4
36y-16x=-80
-7y+16x=80
Even if the first equation has changed, it is still an equivalent equation.Now we add the equations to eliminate the x variable.
36y-16x=-80 +
-7y+16x=80
We get
29y=0
y=0
Substituting y=0 in the equation 36y-16x=-80
36*0-16x=-80
16x=80
x=80/16
x=5
The solution set for the system of equation is x=0,y=5
Solving Quadratic Equations
Quadratic equations are algebraic equations of the form ax2+bx+c=0. They are also known as second degree polynomial equations. The solutions of quadratic equations are known as roots.
Three of the most common ways are Factoring, completing the square and quadratic formula.
Factoring
If a quadratic equation is formulated in such a way that it can be easily divided into two distinct binomials, then we can apply the factoring method to find its roots.
Example
2×2-3x-20=x2+34
First, we bring all the terms of the equation to one side.
2×2-3x-20-x2-34=0
x2-3x-54=0
This can be written as
(x+6)(x-9)=0
Hence,
x+6=0 gives
x=-6
And
x-9=0 gives
x=9
In conclusion, the solutions are x=-6 and x=9.
Completing the square
This method involves transforming the quadratic equation into a perfect square trinomial and then solving for x.
The steps include:
1)Bring the constant to the other side of the equation.
2)Divide both sides by the coefficient of x2 to make the coefficient 1.
3)Add and subtract (b/2a)2 on the left side of the equation.
4)Factor the left side as a perfect square and simplify to find x
Example: x2-6x+5=0
1: Bring the constant term to the other side of the equation.
x2-6x=-5
2: Divide both sides of the equation by the coefficient of x2 :
x2-6x+=-5
3: Add and Subtract (b/2a)2
Here , b=-6, a=1
So the equation becomes
x2-6x+9-9=-5
x2-6x+9=4
= (x-3)2=22
Taking the square root, we get
x-3=2
Therefore, x=3+2 or x=3-2
x=5 or x=1.
These are the solutions for the quadratic equation
Quadratic Formula
This is the quadratic formula
Consider the quadratic equation: 2×2-5x+3=0
First, we identify the coefficients.
Here
a=2
b=-5
c=3
By substituting these values in the quadratic equation, we get
x=3/2 and x=1
So we can say that for the quadratic equation, the solutions are
x=3/2
x=1.
A second-degree equation will have two solutions.
Solving System of Equations
A system of equations can be considered a collection of equations consisting of the same set of variables.
Example –
Consider the system of equations:
2x+3y=10
x-2y=1
1) The substitution method:.
x-2y=1
x=2y+1
2) Substitute this value for the original variable in the other equation.
2x+3y=10
2(2y+1)+3y=10
4y+2+3y=10
7y=8
y=8/7
If y=8/7 then
x=2y+1
x=2(8/7)+1
x=23/7
Simplifying Algebraic Equations
An algebraic equation can be simplified using different mathematical operations such as combining like terms and performing basic arithmetic operations.
For example take the equation
2x2 + 5x – 2x2 +y = 0
After simplification the equation looks like this.
5x+y=0
Equations with Fractions and Decimals
Solving algebraic equations involving fractions and decimals requires similar principles to solving equations with whole numbers. However, extra care must be taken to handle fractions and decimals throughout the process properly.
How to to handle complex expressions involving fractions
For simplifying the equation you may decide to eliminate the fractions by multiplying both sides of the equation by the denominators’ least common multiple (LCM). Similar to this, you might multiply both sides of the equation by a power of 10 to get rid of any decimals if it contains any.
Word Problems and Algebraic Equations
A word problem in algebra is a real-life problem that can be converted into an algebraic equation and subsequently worked on to arrive at solutions for the variables.
The word problem has to be carefully analyzed and variables, constants and coefficients should be identified from it. This should be used to formulate an algebraic equation from the word problem.
Question 1
John’s age is 5 years more than twice Mary’s age. The sum of their ages is 41. How old are John and Mary?
John’s age=x
Mary’s age=y
The equations are
x=2y+5
x+y=41
By substitution method we get y=12
Then, x= 2*12+5=29.
Solving Equations with Exponents and Radicals
An equation containing terms with a variable in the radicand is called a radical equation.
Techniques to simplify and solve equations with these components
- Isolate the radical expression from the equal sign on one side. Put every last term over there on the other side.
- Square both sides of the equation if the radical is a square root. Raise both sides of the equation to the third power if it is a cube root. In other words, increase both sides to the nth power for a radical with the nth root. By doing this, the radical symbol is removed.
- Solve the equation you get.
- Repeat steps 1-2 if a radical phrase still exists.
- You can check your answer by substitution in the original equation.
Advanced Algebraic Equation Solving
Polynomials and solving polynomial equations
Throughout this lesson, we have highlighted how to solve polynomials in various equations. The key is to practice as much as you can, and remember the formulas.
Rational expressions and equations
The quotient of two polynomials is an expression that is rational. An equation is considered a rational equation if it contains at least one rational expression.The denominator of rational formulas usually includes a variable. Hence the denominator cannot be 0.
Steps to solve a rational equation
- Factor all denominators to determine the LCD.
- Multiply both sides of the equal sign by the LCD. Everything should be multiplied so that the fraction is removed.
- Solve the resulting equation
Inequalities and their solution methods
Inequalities contain the signs >, <, ≥ and ≤. When you solve inequalities, you figure out a range of solutions that will make the equations true.
You need to remember the following when solving an inequality
- you can add the same quantity to each side
- you can subtract the same quantity from each side
- you can multiply or divide each side by the same positive quantity
Tips and Tricks for Efficient Equation Solving
- Remember the PEMDAS sequence – Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction. This is the order you should follow.
- Make sure you reduce the equations to the simplest form.
- Use substitution and elimination wherever applicable.
- Practice as much as you can, so that you get used to solving questions.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Any mathematical expression that contains variables and constants along with algebraic operations (addition, subtraction, etc.) is known as an algebraic expression.
- In an algebraic equation, variables denote unknown values. The variables are usually letters of the alphabet, such as x, y, a, b etc.
- Coefficients are the numerical values that are multiplied by variables in an algebraic expression or equation.
- Constants are numerical values that remain unchanged in algebraic equations. A constant does not have any variables attached to it.
- A linear equation is one in which the greatest power of the variable is consistently 1. It can also be referred to as a one-degree equation.
- A quadratic equation is an algebraic equation in which the highest power of the variable is 2.
Quiz
Question comes here
Frequently Asked Questions
Consider a system of equations with two linear algebraic equations with the variables x and y. The substitution method in algebra is used to solve a system of linear equations by substituting the variables.
For example
2x+3y=10
x-2y=-1
Solution
x=2y+1
Substitute this value for the original variable in the other equation
2x+3y=10
2(2y+1)+3y=10
4y+2+3y=10
7y=8
y=8/7
If y=8/7 then
x=2y+1
x=2(8/7)+1
x=22/7
A quadratic formula is an equation that provides solutions for quadratic equations. The formula is
An algebraic equation can be simplified using different mathematical operations such as combining like terms and performing basic arithmetic operations.
Consider:
2x2+ 5x- 2x2 +y=0
After simplification the equation looks like this.
2x2-2x2+5x+y=0
5x+y=0
A word problem in algebra is a real-life problem that can be converted into an algebraic equation and subsequently worked on to arrive at solutions for the variables. We recommend you refer to the word problems mentioned above.
Algebraic inequalities are mathematical statements that express a relationship between two algebraic expressions using inequality symbols such as <,>, ≤ or ≥.
Solving algebraic inequalities involves finding the range of values for the variable(s) that make the inequality true.
Consider the equation: 2x+3>7
On simplification x>2
To check whether the inequality is true or not, substitute any number greater than 2 for x and check whether the equation still stands.
Take x=3
2x+3>7
6+3>7
9>7 is true. Hence, we can say that the inequality is true.
You can solve algebraic equations involving fractions and decimals the way you solve with whole numbers.
For simplifying the equation you can choose to eliminate the fractions by multiplying both sides of the equation by the denominators’ least common multiple (LCM). You can also multiply both sides of the equation by a power of 10 to get rid of any decimals if it contains any.