Exploring the World of Scalene Triangles: Definitions, Properties, and Formulas.
Comprehensive Definition, Description, Examples & Rules
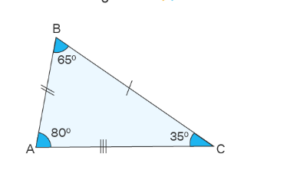
Triangles can be intimidating, and dealing with their types and calculations can test the best of students. Edulyte offers to empower your understanding of triangles, starting from finding the answers to your questions: what is a Scalene triangle? Is it an irregular triangle?
Introduction
Triangles are fundamental geometric shapes in Euclidean geometry, consisting of three sides and three angles. They are essential in various mathematical and scientific disciplines and are the building blocks for more complex geometric structures.
Did you know there are several types of triangles based on their side lengths and the measures of their angles? One such type is the scalene triangle.
Scalene Triangle Definition:
- A scalene triangle has all three sides of different lengths.
Characteristics:
- None of the angles are equal.
- All three sides are of different lengths.
Properties:
- Since the sides are unequal, the scalene triangle angles opposite these sides are also unequal.
- Note that the sum of all interior angles of a triangle, including a scalene triangle, is always 180 degrees.
Example:
If the lengths of the sides are a, b, and c, with a ≠ b ≠ c, then the triangle is scalene.
What is a Scalene Triangle? Definition and Characteristics That You Should Know
Let us find the answer to your question: what is a scalene triangle? A scalene triangle definition states that it is a geometric figure with three sides of different lengths.
Characteristics:
- Unequal Side Lengths: The defining characteristic of a scalene triangle is that all three sides have distinct lengths.
- Unequal Angles: Since the sides are of different lengths, the scalene triangle angles opposite these sides are also different.
- No Symmetry: Scalene triangles lack symmetry in equilateral and isosceles triangles, where at least some sides or angles are equal.
Comparison with Other Types of Triangles:
- Equilateral Triangle: Its three sides are of equal length, unlike a scalene triangle.
- Isosceles Triangle: Its two sides are of equal length and, consequently, two equal angles, unlike a scalene triangle, do not exhibit such symmetry.
Properties of Scalene Triangles
We already know that, as per the Scalene triangle’s definition, it has three unequal sides and angles. Here are some fundamental properties of a scalene triangle:
Unequal Side Lengths:
- The most defining property of a scalene triangle is that all three sides have different lengths.
- Denoting the lengths of the sides as a, b, and c (where a ≠b ≠ c), where no sides are equal.
Unequal Angles:
- Regarding scalene triangle angles, The angles opposite these sides also differ due to the unequal side lengths.
No Symmetry:
- Unlike equilateral and isosceles triangles, scalene triangles lack any form of symmetry in terms of side lengths or angles.
- There is no axis of symmetry, and the triangle’s appearance is asymmetrical.
Scalene Triangle Angles: Easy Explanation of Angles
All three angles are different in a scalene triangle, and their measures can vary widely. The variability in angle measures contributes to the versatility of scalene triangles.
Variability of Angles:
- The angles in a scalene triangle are denoted as A, B, and C, opposite sides a, b, and c, respectively.
- Because all three sides are of different lengths, the corresponding angles are also different: A≠B ≠ C.
The Sum of Angles:
- The sum of the interior angles in any triangle, including a scalene triangle, is always 180 degrees. The equation A+B+C=180 expresses it∘.
Acute, Obtuse, or Right-Angled:
- Depending on the measures of its angles, a scalene triangle can be classified as acute-angled, obtuse-angled, or right-angled.
- An acute-angled scalene triangle has all angles less than 90 degrees.
- An obtuse-angled scalene triangle has one angle greater than 90 degrees.
- A right-angled scalene triangle has one angle equal to 90 degrees.
Versatility in Shape:
- The variability in angle measures gives scalene triangles a diverse range of shapes.
- For example, one scalene triangle might have two relatively small angles and one large angle, making it obtuse-angled, while another might have three moderate angles, making it acute-angled.
Obtuse Scalene Triangle: Definition And Characteristics
An obtuse scalene triangle is a type of scalene triangle that includes one angle measuring more than 90 degrees, making it an obtuse-angled triangle.
Definition:
- An obtuse scalene triangle has three unequal sides and one obtuse angle. “obtuse” refers to an angle measuring more than 90 degrees.
Characteristics:
- Three Unequal Sides: Like any scalene triangle, an obtuse scalene triangle has all three sides of different lengths.
- One Obtuse Angle: The defining characteristic is that it includes an obtuse angle. This angle is greater than 90 degrees but less than 180 degrees.
- Two Acute Angles: The other two angles in the triangle are acute, meaning they measure less than 90 degrees.
Obtuse Angle within the Triangle:
- The obtuse angle in an obtuse scalene triangle is typically denoted as C if c is the longest side (opposite the obtuse angle).
- The sum of the interior angles in any triangle is always 180 degrees. In an obtuse scalene triangle, the obtuse angle C contributes more than 90 degrees to this sum.
Geometric Properties:
- The obtuse angle introduces an interesting geometric property, as it creates a more stretched or elongated appearance to the triangle compared to acute-angled triangles.
- The longer side (opposite the obtuse angle) is also the longest in the entire triangle, contributing to the asymmetry of the triangle.
Applications:
- Obtuse scalene triangles can be encountered in various real-world scenarios and geometric problems.
- In trigonometry, the relationships between the side lengths and angles in an obtuse scalene triangle can be explored using trigonometric functions.
Scalene Triangle Formula: Step-by-step explanation of the formula
The scalene triangle formula is calculated with a base “b” and height “h”, which is “(1/2) bh”.
Or,
Area of a Scalene Triangle = [(1/2) × base × height] square units
Given:
- Base (b) = 8 units
- Height (ℎ) = 6 units
Formula:
A=1/2×base×height
Calculation:
A=1/2×8×6
A=1/2×48
A=24
Result:
The area of the scalene triangle is 24 square units.
Calculating Scalene Triangle Area: Sample Calculations
Review the examples of how to be a pro at handling Scalene Triangle Area calculations.
Example with Scalene Triangle Formula:
Suppose you have a scalene triangle with a base (b) of 10 units and a height (ℎ) of 5 units.
Given:
- Base (b) = 10 units
- Height (ℎ) = 5 units
Formula:
A=1/2×base×height
Calculation:
A=1/2×10×5
A=1/2×5
A=25
Result:
The area of the scalene triangle is 25 square units.
Example with Scalene Triangle Formula
Consider a scalene triangle with a base (b) of 12 units and a height (ℎ) of 8 units.
Given:
- Base (b) = 12 units
- Height (ℎ) = 8 units
Formula:
A=1/2×base×height
Calculation:
A=1/2×12×8
A=1/2×96
A=48 square units
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A scalene triangle is a type of triangle with three sides of different lengths, distinguishing it from equilateral (equal sides) and isosceles (at least two equal sides) triangles.
- An obtuse scalene triangle features one angle measuring more than 90 degrees, contributing to its asymmetrical appearance.
- Area Calculation:
- A =1/2×base×height
- Unlike equilateral or isosceles triangles, scalene triangles cannot exhibit symmetry due to the absence of equal sides or angles, making them inherently asymmetrical.
Quiz
Question comes here
Frequently Asked Questions
Scalene vs. Equilateral Triangles: In a scalene triangle, all three sides have different lengths. In contrast, an equilateral triangle has three equal sides.
Scalene vs. Isosceles Triangles: In a scalene triangle, all three sides and angles are different. In an isosceles triangle, two sides and their opposite angles are equal.
An obtuse scalene triangle includes one obtuse angle (measuring more than 90 degrees) and two acute angles (each measuring less than 90 degrees). The sides of an obtuse scalene triangle are of different lengths.
There is no specific formula for the angles of a scalene triangle because the angles vary depending on the lengths of the sides. The sum of the interior angles of a triangle, including a scalene triangle, is always 180 degrees, but the measures of individual angles are not fixed.
No, a scalene triangle cannot be symmetrical. Symmetry implies that a figure has at least one symmetry or rotational symmetry axis, leading to equal or congruent parts. Since all sides and angles of a scalene triangle are different, there is no way for it to exhibit symmetry.