Circle Area Masterclass: Unveiling the Formula, Tips, and Applications
Comprehensive Definition, Description, Examples & Rules
Introduction to Circle Area Calculation
The area of a circle is the area enclosed by a circle with its radius and circumference. There are numerous circular objects in real life whose area you need to calculate, and it is very useful to calculate the region occupied by a circular plot. The area of a circle formula is also very useful for civil engineers. There are many circular shapes that they have to design, and calculating the area of these shapes is a primary part of that job.
Usage:
- If you want to calculate the area of a circular field, such as a cricket stadium, then you can use this formula.
- The area of steering wheels or car wheels can be calculated as well.
- You can find the exact size of a cake or a pie, which can be important for bakers.
- Builders need to calculate the area of a circular table or a circular object that has to be fitted inside a specific space.
The Formula for Area of a Circle
The exact formula that you use for finding out the area of a circle is:
- A = πr²
‘A’ is the area of the circle. ‘r’ is the total radius of the circle.
When calculating the area of a circle, π (pi) is a crucial value. It is an approximate value that helps determine the precise area covered by the circle.
Significance of π(pi) in the formula:
- It is the ratio of the circumference and the diameter. It is a number larger than three.
- It helps us to understand our universe with proper clarity and has a great notion of measurement of angles.
- It is the primary part of mathematics that represents a constant value, and the exact value of pi is 3.14159.
How to Find Area of a Circle
There are particular steps that you need to follow while calculating the area of a circle.
These are:
- You need to understand that a circle is a two-dimensional shape, and you need to follow the exact formula that is given above.
Find the radius of the circle if the circumference is provided.
- The unit of the area will be in square units, so your answers will be cm² or m²
- The radius of your circle will be exactly half of your circumference.
- Use the π(pi) effectively to calculate, and do not make mistakes.
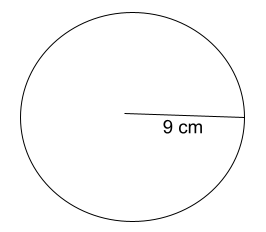
Example: Area of circle with radius
Calculate the area of the circle with a radius of 9 cm
Πr2 = π * 92
A = 254 cm2
Using Diameter to Find Circle Area
The circle’s diameter can also be considered the circle’s circumference, and the radius and the diameter have an inverse relationship. The diameter has a primary role to play while calculating the area of the circle, as in many sums, you will see that the exact radius is not provided, but the circle’s diameter is provided. The radius of a circle is always exactly half the length of its diameter. To find the radius, simply divide the diameter by 2. Understanding this relationship is crucial when calculating the area of a circle or performing other specialized calculations involving circles.
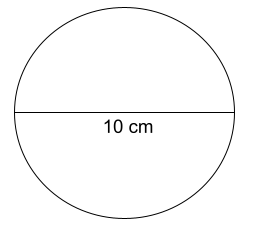
Examples: Area of Circle by Diameter
Find the area of a circle with a diameter of 10 cm
Radius = 5 cm
Πr2 = π * 52
A = 79 cm2
Practical Applications of Circle Area
There are many real-life applications of the area of the circle, and there are many sectors in which you can use the area of the circle. These fields are:
- Geometry: The primary use of the area of the circle happens in geometry. There are many calculations in geometry in which you need to find out the area of a particular shape, and in most situations, you are required to find the area of the circle to determine the entire sum.
- Engineering: The area of the circle is also an essential understanding for civil engineers as they need to calculate the area of a particular shape, and it can be a circle in most situations. Engineers use the basic formula of calculating the area of the circle most often while building the interior designs of a space.
- Design: While designing a place, the designer will require understanding the area of a shape, and in most situations, you have to calculate the area of a circle if you are designing a particular place.
Examples:
- Calculating the area of a dinner plate that has to be used.
- The area that a traffic cone covers on the road.
- Designing a circular shape flower bouquet.
- The area of a circle is essential while making bangles.
Surface Area vs Area of a Circle
There is a major difference between the surface area and the area of a circle. The area of a circle is especially the area of a 2D shape, representing a circular figure. The surface area is the calculation of the area of a 3D shape that might represent a circular shape in three dimensions. The formula used to calculate the surface area of circle is different, and one of the primary examples of a surface area shape is a cylinder that has a circular shape has three dimensions.
Challenges and Complex Shapes
These are:
- Using the formula effectively is an important option; if you mess up the formula, the entire answer will go wrong.
- Challenges might be that you have to break the shape into a half circle, and there are specific formulas that you need to use for that.
You can divide the compound shapes into squares and rectangles, calculate the area of all the shapes, and join them together.
The strategies that can help you to calculate the area of composite shapes are:
- You can break the difficult compound shapes into basic circles, find the area of each circle, and join them together.
- If you break up a shape into a half circle, you can divide the entire formula by two and get the exact area of the half circle.
- If you break down the compound shape into a square or a rectangle, then the formula that you need to use:
- Square: side²
- Rectangle: length × width
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The radius is the most important value you need to calculate for the area of a circle.
- The radius is exactly half of the diameter or circumference of the circle.
- Pi (π) plays an important function in calculating the area of a circle, and the exact approximate value for it is 3.14159.
- You might face challenges while calculating the area of a circle, but you need to use the formula correctly to have the approximate answer.
Quiz
Question comes here
Frequently Asked Questions
If you’re given the diameter of a circle, it’s simple to calculate the radius. The diameter is also known as the circumference, and the radius is just half of that measurement. For example, if the circle’s diameter is 8 cm, the radius is 4 cm, then the area is π4² that is 50.27cm² or 50 cm2 approx.
π(pi) is the most essential value while calculating the area of the circle formula, as it plays a significant role in many mathematical calculations. The exact value of π(pi) is 3.14159.
You have to follow the proper steps to find the area of a circle. These are:
- To find the area of a circle, you first need to know the diameter.
- Divide the diameter by two to find the radius.
- With the radius, you can calculate the area.
- The answer of the area of your circle will be in square units such as inch², cm², m².
The few practical applications of how you can find the area of the circle are:
- The clock is in the form of a circle, and you can calculate the area of that clock while using the hour hand and the minute hand, as you can find the radius with these.
- You can calculate the area of a slice of a pizza by using one of its sides.
- You can divide any circle into multiple sectors and use these sectors to represent the radius and calculate the area.
The formula for the area of a circle is πr²
The formula for the area of the circumference is 2πr
These formulas have a basic difference; the answer will be different amounts.
The answer to the area of the circle will be in square units, while the answer to the circumference will be in single units.