Circle Explained: Definition, Properties, and Calculations
Comprehensive Definition, Description, Examples & Rules
Introduction
Circles are a significant concept in geometry. A circle has an equal distance from a central point. It is rounded in shape and used for various purposes in geometry. In daily life, wheels and plates are common examples of circles. The concept of a circle is used for calculation in math, and in geometry, you can find out the arcs by using circle formulas.
This page will assist you in getting information about the circle’s usefulness and formulas. It sounds interesting, right? So, let’s understand the circle concept from basics to advanced.
What is a circle?
A circle is a rounded shape that has an equal distance from its central points and it is used in geometry.
Define what a circle is and its fundamental characteristics.
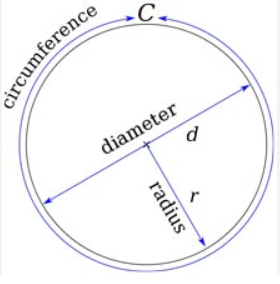
You will find the boundary of the circle at an equal distance from each point. An example of a circle in daily life is a wheel, and so on. A circle consists of a diameter, and half of the diameter refers to the radius.
A circle has basic characteristics like:
- It has an equal distance from the center point.
- A circle contains the diameter and radius.
- It has a circumference that is an outer boundary distance. It is also referred to as 2πr, and the area is πr².
Explain the concept of a circular shape and its uniqueness among geometric figures.
The unique circular concepts are as follows:
- A circle doesn’t have a confined axis of symmetry.
- The circumference of the circle – 360 degrees.
- A circle has an equal distance from all the points.
Understanding Radius and Diameter
Radius and diameter are the most significant elements of a circle. The diameter is the full length, and the radius is the half distance from the diameter.
What is a radius in a circle?
Radius is the half-distance of diameter. It connects the boundary of the circle to the center point.
- R = Diameter/2
Diameter definition in a circle.
The diameter connects the two points of a circle. It divided the circle into two equal sections. Diameter also refers twice to the radius.
- D = radius * 2
Illustrate the relationship between the radius and diameter.
Both diameter and radius are connected to each other. Diameter refers to twice the radius, and the radius is just half the diameter.
Suppose a circle has a 3m radius. When you connect two points of the circle, you will find a 6m diameter, and when you connect the center of the circle to the circumference, you will find a 3m radius. It’s proving the connection between radius and diameter.
Properties of Circle
A circle does have confined axes. You will find an equal distance from the center of the circle. In the following sections, you will learn about circle properties and their significance.
List and explain the key properties of circles, such as symmetry, congruence, and the constant ratio of circumference to diameter (π).
- Symmetry: Circles are symmetrical in shape. You can find the two equal divisions of a circle through symmetry.
- Congruence: Circles have congruence properties, which means two circles can be transformed through a rigid motion series.
- Constant ratio of circumference to diameter: Its symbol is π. This is represented as πD.
Discuss the significance of circles in various fields, including mathematics, science, and engineering
- Mathematics: In mathematics, the concept of a circle is useful in measuring the area, parameters, and circumference.
- Science: In science, you can find the use of the circle concept and its formula for multiple purposes. Circles are also significant in biology and engineering.
- Engineering: In mechanical engineering, the use of circles is significant. It is useful in graphic and circular motion units.
Different Parts of a Circle
A circle consists of different parts that consist of radius, diameter, and so on. You will find a detailed description in the next section.
Describe the various components of a circle, including the center, radius, diameter, circumference, and sectors.
- Center: It is represented with the (O) symbols. That is also known as the origin. It is located at the center of a circle, and the center is helpful in measuring the circle’s circumference.
- Radius: In a circle, connect the center to the circle boundary. It also denotes R = diameter/2.
- Diameter: A diameter is a line connecting two points in a circle that divides the circle into two segments. It denotes D = 2R.
- Circumference: Circumference is the perimeter of a circle. It has the formula 2πr.
- Sectors: It is the inner boundary of a circle that contains the radius and arc of the circle.
Calculating Circumference
Circumference is a parameter of a circle. Its formula is a product of pie and diameter.
- C = π* Diameter
Explain how to calculate the circumference of a circle from its diameter.
You will get to know how to find circumference from diameter by using the formula that is a product of pie and diameter.
C = π* D
It can also be written as 2πr because diameter is double of the radius.
- In this case, C is the circumference.
- Di is a diameter.
- And π is a pi.
Present the formula for finding the circumference of a circle (C = πd) and include practical examples.
Suppose you need to calculate the circumference of a circle with a diameter of 7 meters.
You can solve this sum by using the formula
C = π*d (the value of pi is 22/7)
- C= 22/7*7
- C= 22m
You will find the 22-meter circumference by using the pi value of 22/7.
Finding the area of a circle
In the next section, you will see the formula for the area of a circle.
Introduce the area of circle equation (A = πr²).
- The area of a circle is πr².
- In which π is pi and r is radius.
Provide step-by-step instructions and examples for finding the area.
- You need to find out the radius to calculate the area of a circle.
- After finding the radius, you have to square the radius.
- Then, you have to multiply both the pi and the square of the radius to get the correct answer.
- Assume you have a circle with a diameter of 20cm, and you need to calculate the area of the circle.
You have to apply the A = πr² formula first after finding the radius.
- 10m is a diameter; therefore, the radius would be 10 (20/2).
- Now, the area of a circle would be
= 3.14*10 *10
= 0.0314m².
Defining the Perimeter of a Circle
If you are confused between the perimeter of a circle and its circumference, then you will find the next section interesting.
Define perimeter of a circle and explain its significance.
The perimeter of a circle is significant in finding the distance around the circle. It is the overall distance around the circle boundary.
The formula for the perimeter of a circle = π* D
Now, if you decode the diameter, you will find 2r (r is the radius).
P= 2πr
Differentiate between perimeter and circumference.
Perimeter and circumference sound similar to each other. Let’s understand the common difference between them.
- Perimeter is the distance around the circle, whereas circumference is the distance around the outer area of the circle.
There is no such hard-core difference between both of them.
Offer examples of calculating the perimeter of circles with varying radii.
Suppose you have a wheel with 10cm.
After using the formula for perimeter, you will calculate this as
- P = 2*3.14*10 =6.28cm
Find out the perimeter of a circle with a radius of 7 m.
- P = 2*22/7*7 =44 cm
Practical Applications
The concept of circles is practical in real life. You can use these concepts for multiple purposes and fields.
Explore real-world applications of circles, such as in architecture, art, engineering, and navigation.
- Architecture: The concept of a circle is significant in architecture. It is useful in measuring the dome or circular design.
- Art: It is used by the artist in various arts like kalkari in a circle, mandala art, and so on.
Engineering: In engineering, circles are useful in projects with circular designs.
- Navigation: A circle is useful in navigation as well as through a compass.
Tips and formulas
You can remember the formulas of circles by recalling them every day. You can have a cheat sheet to recall these formals.
Circle | Formulas |
Radius of Circle |
|
Perimeter of circle |
|
Area of circle |
|
Diameter of circle |
|
Share useful tips and tricks for solving circle-related problems.
- You can remember the formulas by recalling them every day.
- You must practice the sums daily. You can also attempt the worksheet given in the frequently asked questions section.
Key formulas and equations related to circles for quick reference.
- P= 2πr
- A= πr²
- R= D/2
- D= 2r
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A circle is a rounded shape that has an equal distance from its central points. In daily life, wheels and plates are common examples of circles.
- A circle is a symmetrical shape that has an equal distance from its center. It is divided into two equal parts.
- A circle contains a center, radius, and diameter that are significant in calculating the area and perimeter of the circle.
- The circle key formulas are P = 2πr, A = πr², R = D/2, and D = 2r.
- Both circumference and perimeter are similar to each other.
- If you want to develop your understanding of this subject, then you need to recall formulas, and you can also practice through the Edulytes worksheet.
Quiz
Question comes here
Frequently Asked Questions
- The radius is half of the diameter: R = D/2
- The diameter is double the radius: D = 2r
That’s how they both are interconnected with each other.
A circle is a symmetrical shape that has an equal distance from its center. It can be divided into two equal parts.
A circle contains a center, radius, and diameter that are significant in calculating the area and perimeter of the circle.
The area of a circle is the product of pi and r. You can take the pi value as 22/7 or 3.14. Suppose you have to find the area of a circle with a radius of 2 cm. You will find the answer 12.57 after using the formula.