
Mastering the Chain Rule in Calculus: Concepts and Applications
Comprehensive Definition, Description, Examples & Rules
Introduction to the Chain Rule:
The chain rule is an essential aspect of mathematics. With the help of the chain rule, we can differentiate composite functions in the field. The chain rule mandates that the derivative of a composite function is equal in measure to the derivative of the outer function that is gauged at the inner function and multiplied by the derivative of the inner function. In mathematical terms, we can denote the chain rule as f(g(x)) = f’(g(x)). The process of chain rule differentiation comes in handy while solving different problems in various interrelated fields like physics, engineering, architecture, and more.
The Chain Rule Formula:
The chain rule maths formula is represented as (f(g(x)))’ = f'(g(x)) * g'(x).
In the formula stated above,
- f is an outer function. In other words, it deals with the output of g(x).
- g is an inner function. In other words, it works with the variable of x.
- f’ is the derivative of the outer function f about its variable u.
- g’ is the derivative of the inner function g about its variable x.
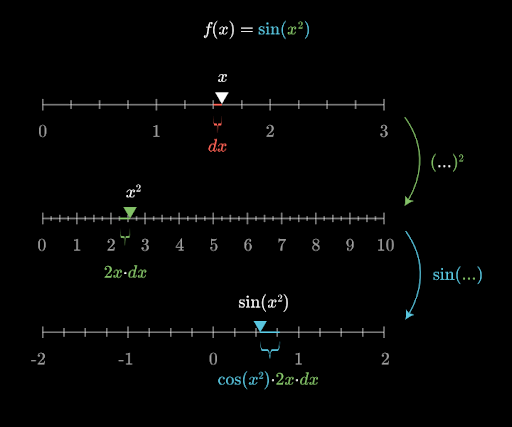
Visualizing the Chain Rule:
Here’s a visual representation of how the chain rule works:
Chain rule examples help to show how composite functions are differentiated. One such example is given below:
Compute the derivative of composite function h(x) = (x3 + 7)10
Solution: Let u = x3 + 7 = g(x), here h(x) can be noted as h(x) = f(g(x)) = u10. So the derivative of h(x) is computed by following the given steps:
d(h(x))/dx = df/du × du/dx
⇒ h'(x) = 10u9 × 3×2
= 10(x3 + 7)9 × 3×2
= 30 x2 (x3 + 7)9
Chain Rule Examples:
Go through the step-by-step examples of how the chain rule is applied to different kinds of functions:
- Trigonometric Functions:
The chain rule is used to distinguish between trigonometric functions that contain another function. The chain rule in differentiation requires one to differentiate the trigonometric function while maintaining the inner function constant, and then multiply by the inner function’s derivative.
The trigonometric functions sin(x), cos(x), and tan(x) can be differentiated using the following rules:
For example, using the chain rule, distinguish cos(2x). Cos(2x) can be expressed as an inner function of 2x and an outer function of cos().
- Step 1: Separate the outside function while keeping the inside function the same.
Cos(x) differentiates to -sin(x), therefore we get -sin(2x) if we keep the inner function as 2x rather than x.
- Step 2: Multiply this by the inner function’s derivative.
2x is the inner function, and its derivative is 2.
f'(x) = -2sin(2x) is obtained by multiplying -sin(2x) by 2.
Trigonometric functions raised to a power can also be subjected to the chain rule:
- In brackets, write the trigonometric function as the inner function and the power as the outer function.
- Reduce the power and subtract one from the power while keeping the trigonometric function constant.
- Multiply this by the trigonometric function’s derivative.
For example, using the chain rule, distinguish sin4(2x).
Step 1: Write sin4(2x) as [sin(2x)]4.
Step 2: Reduce the power and subtract one from it while keeping the trigonometric function constant. When we remove the 4 in front of the brackets, the power becomes 3, and sin(2x) remains inside the brackets, giving us 4[sin(2x)]3.
Step 3: Multiply by the sin(2x) derivative. Using the chain rule, sin(x) is the outer function that differentiates from cos(x). We maintain the 2x within so that we can get cos(2x). This is then multiplied by the derivative of 2x, which is 2.
The differentiated sin(2x) is 2cos(2x).
As a result, we multiply 4[sin(2x)]3 by 2cos(2𝑥).
8sin3(2x)cos(2x) = f'(x)
- Exponential Functions:
The derivative of y = e𝑥 is dy/d𝑥 = e𝑥 and so using the chain rule, the derivative of y = ef(𝑥) is dy/d𝑥 = f'(𝑥).ef(𝑥). The chain rule of differentiation asks to simply differentiate the power of e and multiply this by the original function.
For example, differentiate e5𝑥+3
Solution: In this example, f(𝑥) = 5𝑥 + 3 and so, f'(𝑥) = 5.
To find the derivative of y = e5𝑥+3, we simply multiply it by 5.
We get dy/d𝑥 = 5 e5𝑥+3.
- Logarithmic functions:
The chain rule asserts that dy/dx = 1/u du/dx for y = ln(u). In other words, distinguish the inner function and then divide it by the inner function. For instance, if y = ln(x2 + 3x), dy/dx = (2x + 3)/(x2 + 3x).
1/u du/dx is the derivative of y = ln(u).
u is the function contained within the ln function. u = x2 + 3x for y = ln(x2 + 3x).
As a result, du/dx = 2x + 3.
The derivative dy/dx = dy/dx = 1/ x^2 + 3x *2x + 3
This can also be written as 2x+3/ x^2 + 3x
The chain rule helps us to distinguish between log functions. The chain rule derivative of y = ln(f(x)) is expressed as follows:
f’(x) = 1/f(x)
or dy/dx = f’(x)/f(x)
If y=log_af(x), then dy/dx= f’(x)/log_af(x) to differentiate any log.
For instance, differentiate considering y = log5(2x + 1):
Here, f(x) = 2x + 1, hence f'(x) = 2.
When we plug these into the formula, we get: dy/dx = 2/log_5(2x+1)
Chain Rule Applications:
Chain rule helps solve various practical problems in a lot of real-world applications. For example:
- Physics: In physics, the chain rule is used to compute orbits of gravitational fields that have frequently changing forces.
- Engineering: In engineering, the chain rule is used to analyze and design different electric circuits, mechanical structures, etc.
- Economics: In economics, the chain rule is used to study and analyze functions of production which helps economists to discern how a change in the variable of input brings a change in the output.
Chain Rule for Higher Derivatives:
The chain rule is extended to higher-order derivatives (second, third, etc) by applying it repetitively. The given example will lend you a better understanding of the concept:
Compute the derivative of y= ln √x with the help of the chain rule.
Solution:
y = ln √x.
f(x) = y is a composition of the functions ln(x) and √x and hence can be differentiated using the chain rule.
Assume that u = √x. Then y = ln u.
According to the chain rule formula,
dy/dx = dy/du · du/dx
dy/dx = d/du (ln u) · d/dx (√x)
dy/dx = (1/u) · (1/(2√x))
dy/dx = (1/√x) . (1/(2√x))
dy/dx = 1/(2x) (because u = 1/(2√x)).
y = cos (2×2 + 1).
Final Answer: dy/dx = 1/(2x)
Chain Rule in Multivariable Calculus:
The chain rule calculus generalizes to functions with multiple independent variables in the multivariable calculus or calculus that has more than one variable. The chain rule is needed to calculate partial derivatives, through which we can know how a function changes according to a variable while keeping other variables constant or fixed. This technique helps us calculate derivatives in systems that are complex and difficult to solve. Also, the chain rule helps in determining gradient vectors and directing processes of optimization and vector calculations in different scientific and engineering fields.
Common Mistakes and Pitfalls:
Go through the following mistakes and pitfalls while applying the chain rule to carry out calculations more efficiently:
- Do not forget to multiply by the derivative of the inner function.
- Do not mistake inner functions for outer functions.
You can avoid the mistakes given above by:
- Always differentiating between the inner and outer functions.
- Practice simplifying using algebra daily.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The chain rule in mathematics mandates that the derivative of a composite function is equal in measure to the derivative of the outer function that is gauged at the inner function and also interacts with the derivative of the inner function through the operation of multiplication. In mathematical terms, we can denote the chain rule as f(g(x)) = f’(g(x)).
- The chain rule comes in handy while solving different problems in various interrelated fields like physics, engineering, architecture, and more.
- The chain rule is applied to different kinds of functions like trigonometric, logarithmic, and exponential.
- The chain rule is extended to higher-order derivatives (second, third, etc) by applying it repetitively.
- The chain rule generalizes to functions with multiple independent variables in the multivariable calculus or calculus that has more than one variable.
- You can avoid the mistakes while using the chain rule by following the given steps:
- Do not forget to multiply by the derivative of the inner function.
- Do not mistake inner functions for outer functions.
- Always differentiating between the inner and outer functions.
- Practice simplifying using algebra daily.
Quiz
Question comes here
Frequently Asked Questions
You can apply the chain rule by differentiating the outer function and multiplying it with the derivative of the inner function.
Suppose you’re given y = (3x^2+5^2)^5. You can solve this by finding dy/du = 5u^4 and dy/du = 6x. When you multiply these conclusions, you get dy/du = 30x(3x^2+2)^4.
Some common mistakes to avoid when using the chain rule are:
- Do not forget to multiply by the derivative of the inner function.
- Do not mistake inner functions for outer functions.

