Unlocking the World of Polygons: Shapes, Definitions, and Formulas
Comprehensive Definition, Description, Examples & Rules
Introduction to Polygons
Polygons are fundamental shapes in geometry that consist of flat, closed figures formed by connecting three or more line segments. Unlike curves, polygons have straight sides. They can have any number of sides, making it difficult to determine the specific quantity.
Significance in Geometry
The major significance of polygons in geometry are:
- A polygon is a closed shape in geometry.
- The beginning and end of the shape meet at a specific point.
- This characteristic is what gives the polygon its primary significance.
Polygon Shapes
There are various types of polygon shapes, and these are:
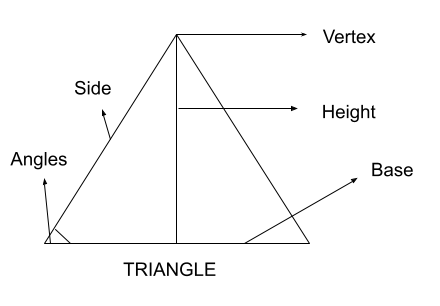
Triangle
Among the most common polygon shapes, a triangle is one of them. It is the simplest polygon form, consisting of three sides with three vertices. Classifying the triangle into different types according to its angle and the sides is also possible.
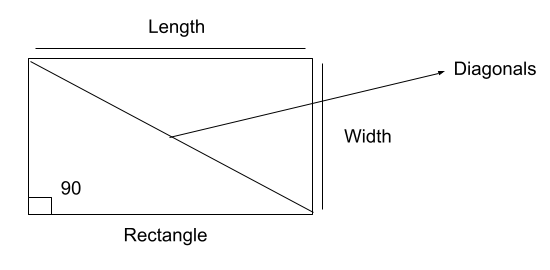
Rectangles
Another common geometrical shape is a rectangle, which is also considered to be a polygon. It is a two-dimensional closed polygon that has opposite sides equal in length and are parallel to each other. It is an irregular polygon with equal angles of 90 degrees each but unequal sides.
Pentagons
A pentagon can also be considered a polygon consisting of five sides and five angles. The Pentagon is one of the rare polygons that consists of different angles, but the sides of the Pentagon can be equal in most scenarios.
The other polygon shape examples are:
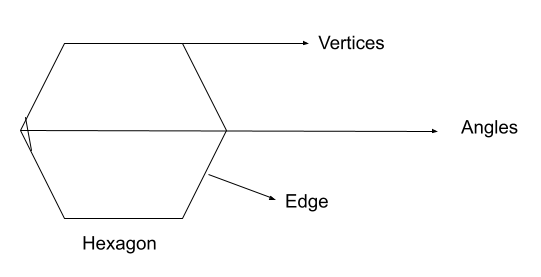
- Hexagon
- Quadrilateral
- Decagon
- Heptagon
- Octagon
Polygon Definition
A polygon is a closed figure in a two-dimensional plane formed by connecting line segments. It has straight sides and has at least three line segments, but it can also have more. A polygon’s starting and ending points are the same, making it a closed shape, and it cannot contain any curved sides.
Characteristics and Properties
The primary characteristics and properties of the polygon shape are:
- A polygon can always consist of three or more sides.
- In a regular polygon, all interior angles and sides are equal.
- Additionally, the sum of its exterior angles always adds up to 360°.
What is A Polygon Shape?
A polygon shape is a two-dimensional figure with a closed figure of line segments. It is the answer to what’s a polygon. Eventually, this means that none of the sides of a polygon are open, and it consists of a minimum of three line segments that make a closed figure.
All the line segments we use to make a polygon have straight lines, and no curve shapes are used. It is one of the most essential features to define that a polygon consists of all straight sides, and none of the sides of the polygon has any curve shape.
Common Types of Polygons
There are specific well-known types of polygons that you use in regular geometrical equations, and the types of these polygons are:
- Triangle: One of the most commonly used polygon shapes is the triangle. The triangle is the most basic polygon, composed of three sides and three vertices. A triangle can be classified as regular when all its sides and angles are equal. However, triangles can also have different types based on the varying lengths of their sides and measurements of their angles.
- Hexagons: The necessary geometry shape and specific unique features make it a very attractive shape. The hexagon is a two-dimensional closed figure with six sides and six vertices, and you can classify it as a polygon. It consists of being of the same length, and the internal angles of the hexagon are similar, making it a regular polygon.
- Quadrilaterals: Any closed shape with three or more sides is considered a polygon. It is the broader version of a square or a rectangle, consisting of four sides and four vertices. A square is a type of quadrilateral, which you can say to be a regular polygon, while a rectangle is a quadrilateral, which you can classify as an irregular polygon.
Polygon Formulae
You might be required to calculate the perimeter and the area of all the different types of polygons. The formula to calculate the area and perimeter of different shapes are different. The formula of polygons include:
Triangle
- Area: ½ × base × height
- Perimeter: Side + Side + Side
Rectangle
- Area: length × breadth
- Perimeter: 2 ( length + breadth)
Square
- Area: side ²
- Perimeter: 4 × side
Hexagon
- Area: {(3 × √3)/2} side²
- Perimeter: 6 × side
You have to use these formulas for calculating the area and perimeter for certain common polygons.
Infographic: "Polygonal Marvels"
The diagrams of various types of Polygons are:
Exploring Regular vs. Irregular Polygons
There is a basic difference between the regular and the irregular polygons regarding their characteristics and sizes. For a regular polygon, all the sides of the shape are equal, and all the shapes’ angles are equal to each other. On the other hand, irregular shapes do not consist of equal sides, and the angles of the shapes are not equal.
One of the major examples of a regular polygon is a square or, in a situation, a triangle. An example of an irregular polygon will be a rectangle or a right-angle triangle with different angles and sides.
Applications of Polygons
There are various aspects in the real world where you can use polygons. These are:
- Urban Planning: Urban planning relies heavily on the shape of polygons as they represent essential elements and require precise calculations. In the current context, it is a crucial sector that encompasses various necessary functions and products.
- Architecture: One of the primary areas where you can use the polygons is architecture to build a new building. You can use a polygon shape to form different shapes, which helps in architecture and construction in a great way. The architect says to use the polygon shape and its features in most of their constructions.
- Art: The artists are also the primary users of geometry and shapes, and they focus on using polygons in most of their artistic figures, helping them to give an aesthetic look.
- Tessellation: A tessellation is a set of highly symmetrical shapes and uses regular polygons to create a particular set of shapes.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A polygon is one of the most common shapes in geometry, and the necessary shapes in geometry are considered to be polygons.
- It is a closed shape, with no curved sides in a polygon.
- The calculation of area and perimeter for different polygons is different, which you must follow through this blog.
Quiz
Question comes here
Frequently Asked Questions
A polygon is a closed shape, and calculating its perimeter is simple. The perimeter refers to the total length of the shape’s outer boundary, and this calculation varies for different polygons. For irregular shapes, you can add up all the sides to find the perimeter. However, for shapes with equal sides, you can multiply one side by the number of sides the shape has to get the perimeter.
The sum of a polygon’s interior angles is always 180 degrees. The value of the exterior angles of the polygon I change according to the number of angles present inside the polygon.
There are specific real-world examples of polygons, and these are:
- Triangles
- Pyramids
- Windows
- Box
- Laptop
- Television
- Diamond
The major importance of polygons in geometry. These are:
- They teach how to make particular shape patterns and use the polygons to make other shapes.
- The polygons help to build symmetry, and joining them together allows you to make different three-dimensional shapes.
- The symmetry of the polygon is very attractive, which makes geometry calculations very easy.