
Unlocking the Power of Compound Interest: Formulas and Calculations
Comprehensive Definition, Description, Examples & Rules
Introduction to Compound Interest:
It is a basic concept in finance that is equally important for people. Compound interest is calculated on the principal amount. This interest rate accumulated over the previous period. It’s a significant concept in banking, investing, and so on. You will learn about the formulas for compound interest, their significance, and so on.
Compound interest is the addition of the rate of interest to the principal sum of a loan or any deposit. If you want to grow your investment, then compound interest is significant.
There are various benefits to compound interest, such as:
- Compound interest is helpful for investment growth. It is a process of reinvesting in your principal amount that also increases the interest rate.
- You can also grow your savings through compound interest.
- You can understand the loan management system through compound interest.
How compound interest differs from simple interest.
Compound interest and simple interest are different from each other. Simple interest is calculated on the principal amount. There is no change in interest paid in simple interest. The simple interest formula is P*R*T. P is the principal, rate is the rate of interest, and t is the timing.
On the other hand, compound interest is calculated on the principal amount. This interest rate accumulated over the previous period. Annual compound interest formula is A = P(1 + r/n)^(nt).
The compound interest formula:
We have discussed the meaning of compound interest. It is a rate of interest calculated on the principal amount.
Present the compound interest formula :
The formula for compound interest is:
A = P(1 + r/n)^(nt).
In this formula, A is the total amount of money after compound interest.
P is the principal amount.
R is the annual rate of interest.
N is the compound interest frequency in terms of time.
T is the time period of compound interest.
Significance:
- The principal amount is the borrowing or investing amount.
- The annual rate is the rate at which your money grows.
- Compounding frequency is necessary for calculating the interest rate in a year.
- A time period is a specific duration of interest rate in borrowing or investment on which your money grows.
Annual compound interest calculation:
Annual compound interest can be calculated easily by using its formula. On an annual basis you can calculate compound interest on an annual basis, like:
For the second year, compound interest after using this formula would be P(1 + r/n)^(nt). Now, to find out the compound interest, you have to use CI = P (1 + r/n)nt – P by subtracting the principal amount from the compound amount.
You can calculate the compound interest on an annual basis like this:
For the first year:
P = 10,000
Time = 1 year
Interest = 1000
For the second year:
P = 10000 + 1000 = 11000
Time = 1 year
Interest = 1100
For the third year
P = 11000 + 1100 = 12100.
Time = 1-year
Interest = 1210
Practical examples and step-by-step calculations.
Step 1: You need to consider the principal, rate, and time period given.
Step 2: Students can calculate the amount with the compound interest formula.
A = P(1 + r/100)n
Step 3: Students can find compound interest using the formula CI = amount minus principal
For example,
Assume you have invested 10,000 INR in a savings account with an annual rate of 6% within the time period of 5 years. Calculate compound interest!
From the given statement, you need to observe the
Principal amount: 10,000 INR,
Rate of interest: 6%
Time period: 5 years
Then, you need to use the formula A = P(1 + r/n)^(nt).
Amount= 10,000(1+6/100) ⁵
10,000(1.06)⁵
10,000*1.33822 = 133882.2
Therefore, the amount would be 133882.2 in your savings account after five years.
Quarterly compound interest calculation:
Quarterly compound interest is similar to that of annual interest. Quarterly, you will find the interest rate at four years.
The Quarterly compound interest formula is
A = P(1 + r/n)^(nt).
The compound interest rate is a 4-year time period rate. You won’t find any dissimilarity between the annual and quarterly rates; only the time period would be fixed in the quarterly time period.
Its formula is:
A = P(1 + r/n)^(nt).
Real-world scenarios
For example:
Assume that you have 10,000 INR in your account at an interest rate of 6 with a 5-year time period.
From the given statement, you need to observe the
Principal amount: 10,000 INR
Rate of interest: 6%
Time period: 5 years
compound interest frequency: 1
A= 10,000(1+0.06/1)¹*⁵
10,000(1+0.06)*⁵=13.392
13.392 is annual compound interest.
After calculating on an annual basis, you need to calculate on a quarterly basis:
Principal amount: 10,000 INR
Rate of interest: 6%
Time period: 4 years
compound interest frequency: 4
10,000(1+0.06/4)⁴*⁵
10,000(1+0.015)²⁰ =13459.3
13459.3 is quarter-compound interest.
Compound Interest vs. Simple Interest:
Compound and simple are the different methods of calculating investment and savings. You will find the comparison between both of them in this section.
A simple interest rate is calculated on the principal amount over a period of time without any change. On the other hand, compound interest is calculated on the principal amount. This interest rate accumulated over the period.
Both simple interest and compound interest have different formulas.
- Simple interest rate: P*R*T
- Compound interest rate: A=p(1+r/n)^nt
- Simple interest rates are not beneficial for investment purposes in comparison to compound interest rates.
- If you invest for a longer period in compound interest, then you may find better investment results.
How compound interest can lead to higher returns on investments.
A compound interest rate helps grow the investment. In compound interest, the interest rate gets accumulated on the principal amount, which gives individuals higher benefits and a higher return on investment.
The Power of Time in Compound Interest:
Time has a significant role in the compound interest rate. It is important for investment growth overall.
The role of time (t) in compound interest calculations.
If you invest for a longer period, then you will receive better returns.
For example, if you invest for a shorter period of time, you will receive a lower return.
If you invest for a longer period of time, like ten years, then you may receive higher returns.
Examples
If you will invest your 10,600₹ for one year, then you may get a 600 interest rate.
- If you invest for ten years on 18,000 rupees, then you may get the 8,000 interest rate.
That’s how the long-term can help you get higher results.
Compound Interest in Practice:
The compound interest concept is relevant in present life. It is useful in various sectors, including finance and banking.
Practical applications
- Personal finance: compound interest is beneficial in emergency funds because you can invest your money for a longer period of time as an emergency fund that can give you a good amount of return after a specific period of time.
- Savings account: You can have growth in your savings account investment. You will get a return after compound interest.
- Investment: You can purchase shares or invest in the stock market. You can also get high returns through mutual funds and other compound interest sources.
- Loans: While taking a loan, you need to consider borrowing for a shorter period of time. Because it’s a compound amount, it can be a problem for you.
Compound Interest Frequency:
Compound interest may affect savings and investments. You can grow your money through compound investing.
- Annually: In annual compounding, the rate of interest can be calculated once a year.
- Quarterly: In quarter compound interest, the rate of interest is calculated four times in the year.
- Monthly: In a month, compounding the rate of interest calculated on a monthly basis is 12 months.
Assume a principal amount of ₹10,000 with a 6% rate of interest and a time duration of 5 years.
- For annual compounding, you will get 10,000 (1+0.06)⁵=13392.7.
- For quarter-compounding, you will get:
10,000(1+0.06*4)⁴*⁵=13459.3
For monthly compounding
10,000(1+0.06/12)*¹²*⁵ =13515.8
You can observe the sharp difference between all three compound scenarios. You can observe the higher and lower compound interest rates on the basis of frequency.
Visualizing compound interest:
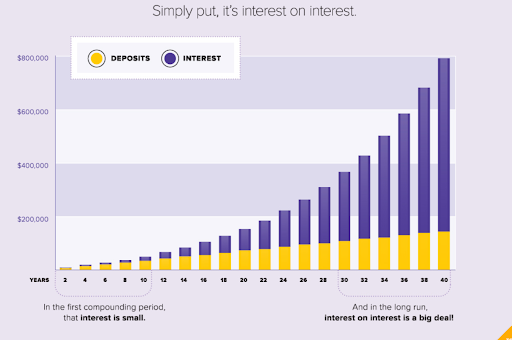
Common Mistakes to Avoid:
There are various common mistakes that students commit:
- Students forget the use of appropriate formulas.
- Sometimes, students get confused between compound amounts and principal amounts.
- Students get confused with the quarter and monthly time periods of compound interest.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Compound interest is calculated on the principal amount. If you want to grow your investment, then compound interest is significant.
- The formula for compound interest is
- A = P(1 + r/n)^(nt).
- Quarterly compound interest is similar to that of annual interest. Quarterly, you will find the interest rate at four years.
- There is monthly compound interest as well which is important for investment growth
- You can improve your compound interest concept by practicing on a daily basis.
Quiz
Question comes here
Frequently Asked Questions
You will grow the investment of your money if you invest for a longer period of time. You can invest in a monthly compound interest to get better returns.
If you invest 10,000 with a 5% interest rate, you may receive 12763.9 INR, and if you invest on a quarterly basis, you will get a return of 12,830.7 INR.
The annual compound interest rate is once a year, and the quarterly compound interest rate is calculated four times a year.
By investing your amount in quarterly or monthly compounding, You can receive a higher return rate.
Compound interest is applied to loans and debts; that’s why it is recommended that you take a shorter period of loan charged with a compound interest rate.

