Exploring Central Angles in Circles: Formulas and Concepts
Comprehensive Definition, Description, Examples & Rules
Introduction
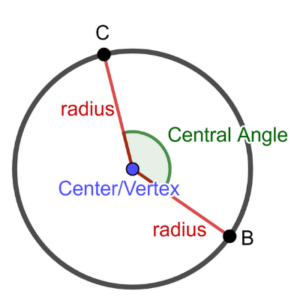
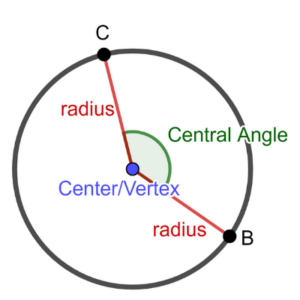
As the name suggests, the angle that is formed at the midpoint of a circle is the central angle. A central angle has its vertex at the midpoint of the circle and defines the length of an arc (a part of the circle’s circumference). The measurement of a central angle is directly proportional to the arc it subtends and their relationship can be explained with the formula: central angle = length of the arc/radius of the circle. The central angle has a crucial role to play in a variety of fields like trigonometry and geometry as it helps carry out several important calculations and solve complex problems.
In the following article, we will come across everything there is to know about a central angle and its properties, formulas, applications, theorems, and more.
What is a Central Angle?
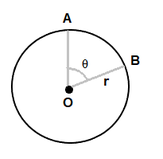
The central angle of a circle is the angle is the angle that is formed at the midpoint of a circle. The length of an arc (a section of the circle’s circumference) is defined by a central angle, which has its vertex at the middle of the circle. The central angle can be computed by dividing the length of the arc by the radius of the circle.
We know that a circle can be sectioned equally into 360 parts in total. In other words, a complete round around the circle will be equal to 360 degrees, and other angles that are smaller than this are subsequent parts or multitudes of this value. So a right angle is 90 degrees, a straight angle is 180 degrees, etc.
Central Angle of a Circle Formula
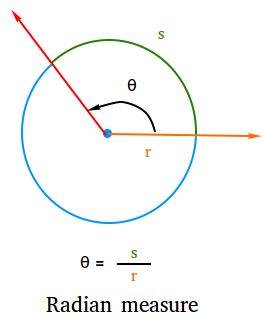
The central angle of a circle formula is represented as:
θ = s / r
Here,
- θ: The central angle of the circle.
- s: The length of the arc of the circle subtended by the central angle.
- r: The radius of the circle.
Here are some examples to help you understand the central angle of a circle formula better:
1. Calculate the central angle of a circle with an arc length of 20 cm and a radius of 4 cm.
Solution: The central angle of a circle formula states that the central angle can be calculated as:
θ = 20/4
θ = 5
Hence, the central angle is 5 radians.
2. Calculate the central angle of a circle with an arc length of 64 cm and a radius of 8 cm.
Solution: According to the central angle of a circle formula, the central angle can be calculated as:
θ = 64/8
θ = 8
Hence, the central angle is 8 radians.
Understanding Angles of a Circle
Here is a list of the different types of angles of a circle:
- Central Angle: The angle that is formed at the midpoint of a circle is the central angle. A central angle has its vertex at the midpoint of the circle and defines the length of an arc (a part of the circle’s circumference). The measurement of a central angle is directly proportional to the arc it subtends and their relationship can be explained with the formula: central angle = length of the arc/radius of the circle.
- Inscribed Angle: An angle that is formed by two chords that have a common endpoint on the circle is an inscribed angle. The measurement of an inscribed angle is half the measurement of the obstructed arc. The same arc is subtended by inscribed angles.
- Interior angle: An angle that is constructed inside the circumference of a circle is an interior angle. The length of the chords determines the measurement of an interior angle.
- Exterior angle: An angle that is formed outside the circumference of a circle is an exterior angle. Half of the difference between the two obstructed arcs is the measurement of an exterior angle.
- Tangent-Chord Angle: An angle that is formed by a tangent and a chord that meets at a point on the circumference of the circle is a tangent-chord angle. The measurement of a tangent-chord angle is half the measurement of the obstructed arc.
Here’s how central angles differ from other circle-related angles. While a central angle is formed at the center, inscribed angles are formed by chords, interior angles are formed inside the circle, exterior angles are formed outside the circle, and tangent-chord angles are formed by a tangent and a chord.
Properties of Central Angles
Here are certain key properties of central angles:
The unit of measurement for central angles is radian or degree.
The measurement of a central angle is directly proportional to the measurement of the arc it obstructs on the circumference.
The measurement of a central angle is equal to the measurement of the obstructed arc.
All central angles sum up to 360 degrees.
A central angle obstructs the same arc as that subtended by an inscribed angle.
The Relationship Between Central Angles and Circumference
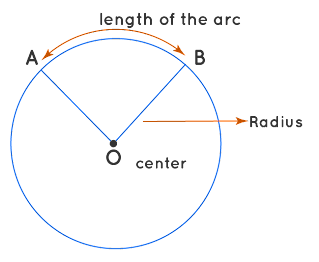
The measurement of a central angle is directly proportional to the length of the arc that is obstructed by it. This is the Angle-Arc Theorem. Mathematically, the length of the arc = (measurement of the central angle / 360) * circumference.
Hence if you know the measurement of the central angle and the radius of the circle, you can easily calculate the length of the arc.
Applications of Central Angles
Central angles find use in a variety of applications in everyday life. They help pilots discern the trails of flight for aircraft and navigate routes in difficult atmospheres, long distances, and other obstacles. In engineering, central angles are used to compute the angles for a smoother and safer development. Furthermore, central angles are used by astronomers when deciding positions for certain stars and satellites, a useful process for space exploration and communication.
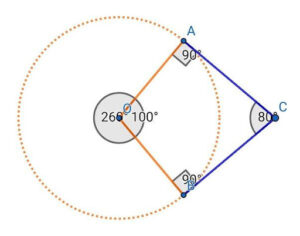
The Sum of Central Angles in a Circle
The sum of all central angles in a circle is always 360 degrees. This conclusion is based on the thought that a complete revolution around a circle amounts to a measurement of 360 degrees. To visually prove this statement, imagine radii starting from the midpoint of the circle until the junctions where the circle meets with the angles. Now, we have a group of triangles with each having its apex at the center of the circle. Since the sum of all angles in a triangle is 180 degrees and since there are two triangles for every central angle of a circle, the sum of all central angles would be 180+180 = 360.
Central Angle Theorems
Theorems related to the central angle in a circle:
- Central Angle Theorem
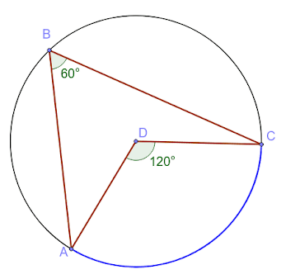
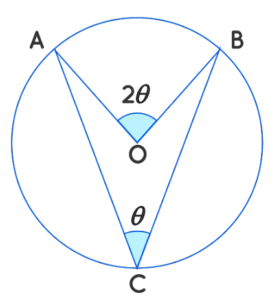
The theorem states that the angle formed at the midpoint of a circle is always twice the measurement of the angle obstructed by the arc on the circle’s circumference.
- Inscribed Angle Theorem
The theorem states that the inscribed angle is always half the measurement of the angle that obstructs the same arc.
Central Angles in Trigonometry
Central angles have a crucial role to play in the field of trigonometry. The coordinates of the junction where the final side meets with the unit circle represent the Sine (sin θ) and Cosine (cos θ) functions. The y-coordinate is represented by the sine function and the x-coordinate is represented by the cosine function. With the help of central angles, trigonometric functions are applied in a variety of fields in real life like mathematics, astronomy, engineering, and more.
Visualizing Central Angles
To understand the central angles and their functions better, you can engage in videos and lectures online and websites that provide you comprehensive knowledge on all the aspects of the subject, like Edulyte. Here are some diagrams to understand central angles better:
Central Angle of a Circle
Angle Subtended by an Arc
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The angle that is created at the midpoint of a circle is the central angle. A central angle has its vertex at the midpoint of the circle and defines the length of an arc (a part of the circle’s circumference).
- The formula to calculate the central angle of a circle is θ = s / r, where, θ is the central angle of the circle, s is the length of the arc of the circle subtended by the central angle, and r is the radius of the circle.
- The measurement of a central angle is directly proportional to the arc it subtends and their relationship can be explained with the formula: central angle = length of the arc/radius of the circle.
- The measurement of a central angle is directly proportional to the length of the arc that is obstructed by it and directly related to the circumference of the circle. Hence if you know the measurement of the central angle and the radius of the circle, you can easily calculate the length of the arc.
Quiz
Question comes here
Frequently Asked Questions
The formula to calculate the central angle of a circle is θ = s / r, where, θ is the central angle of the circle, s is the length of the arc of the circle subtended by the central angle, and r is the radius of the circle.
No central angles have the midpoint of the circle as their apex whereas the angles formed by intersecting lines within a circle (inscribed angles) are formed by two chords that have a common endpoint on the circle.
The measurement of a central angle is directly proportional to the length of the arc that is obstructed by it and directly related to the circumference of the circle. Hence if you know the measurement of the central angle and the radius of the circle, you can easily calculate the length of the arc.
Yes, the sum of all central angles in a circle is always 360 degrees.