Unlocking the Arctan Formula: Mastering the Art of Tangent Inverses
Comprehensive Definition, Description, Examples & Rules
Introduction to Arctan Formula
The opposite or the inverse of the tangent function in geometry is known as the arctangent formula. Mathematically described as arctan (x) or tan^-1 (x), the arctan formula has a range from -π/2 to π/2. The domain of this inverse function of the tangent formula is -∞ < x < ∞. The arctan formula finds various uses in an array of fields seen in everyday life like finding out angles in the field of trigonometry, in geometry, the various calculations of angles and triangles are done with the help of the arctangent formula. Additionally, the arctangent formula is also employed in physics and engineering to find out wavelengths, study motion, etc.
What is Arctangent (Arctan)?
In geometry, the arctangent formula is a reverse of the tangent function. The arctan function is mathematically described as arctan (x) or tan^-1 (x) and does the role of carrying out the exact opposite function of what the tangent function does. In mathematics, when any entity is raised to the power of -1, it represents an opposite or inverse function. Hence, the arctan formula is represented as tan^-1 (x) or the opposite of tan(x).
Arctangent Formula
The arctan function that is symbolized as arctan (x) is used to refer to an angle whose tangent function is x. Hence,
Given that tan(x) = (θ)
arctan (x) = tan^-1 (x) = (θ)
Finding the angle whose tangent has a given value has various important functions in an array of real-life scenarios, like:
- Geometry: Various problems related to geometric shapes like triangles and their angles are solved using the arctan function.
- Trigonometry: The arctan function is used to carry out mathematical operations related to right-angled triangles in trigonometry.
- Computers and Graphics: The arctan formula is used to create and develop various images and effects related to animation and developing games.
Using the Arctan Formula
Here is a step-wise guide on how to find an angle using the arctan formula when a tangent value is given:
- Carefully note the value available in the information provided whose angle you need to compute.
- Employ the arctan formula.
- Solve the equation.
Example
What will be the value of θ if tan(θ) is 0.5?
Solution
It is given that x = 0.5.
So, arctan (x) = arctan (0.5) = (θ)
Arctan (x) = 0.4636 radians or 26.5 degrees.
Practical Applications of Arctan
The arctan formula has a lot of uses in various real-life fields, for example:
- The arctan formula is used to find measures of right angles and right-angled triangles required in various operations of physics.
- The arctan formula can be used to figure out the height of complex shapes and structures in engineering.
- The arctan formula can be used to create compelling effects and animations in computer graphics.
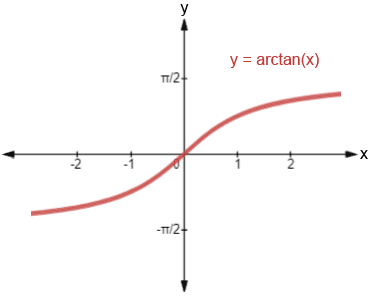
Graphical Representation
Here is a visual representation of the arctan functions, along with its domain and range:
Domain: -∞ < x < ∞
Range: -π/2 < y < π/2
Arctan Identity and Trigonometric Relationships
Here is a list of different identities and properties related to the arctangent:
Arctan Identities
There are various arctan formulas, identities, and characteristics that can be used to solve basic and complex inverse trigonometry sums. A few examples are provided below:
- tan (arctan x) = x, for all real numbers x
- arctan (tan x) = x, for x ∈ (-π/2, π/2)
- arctan(1/x) = π/2 – arctan(x) = arccot(x), if x > 0 or,
- arctan(1/x) = – π/2 – arctan(x) = arccot(x) – π, if x < 0
- sin(arctan x) = x / √(1 + x2)
- cos(arctan x) = 1 / √(1 + x2)
- arctan(-x) = -arctan(x), for all x ∈ R
We also have some arctan formulae for π. These are provided below.
- π/4 = arctan(1/2) + arctan(1/3)
- π/4 = 2 arctan(1/3) + arctan(1/7)
- π/4 = 8 arctan(1/10) – 4 arctan(1/515) – arctan(1/239)
- π/4 = 2 arctan(1/2) – arctan(1/7)
- π/4 = 4 arctan(1/5) – arctan(1/239)
- π/4 = 3 arctan(1/4) + arctan(1/20) + arctan(1/1985)
Arctan Properties
Following are some helpful arctan identities based on arctan function attributes. These formulas can be used to simplify difficult trigonometric statements, making it easier to tackle challenges.
- tan-1x + tan-1y = tan-1[(x + y)/(1 – xy)], when xy < 1
- tan-1x – tan-1y = tan-1[(x – y)/(1 + xy)], when xy > -1
- tan (tan-1x) = x, for all real numbers x
- We have 3 formulas for 2tan-1x
- 2tan-1x = sin-1(2x / (1+x2)), when |x| ≤ 1
- 2tan-1x = cos-1((1-x2) / (1+x2)), when x ≥ 0
- 2tan-1x = tan-1(2x / (1-x2)), when -1 < x < 1
- tan-1(1/x) = cot-1x, when x > 0
- tan-1(-x) = -tan-1x, for all x ∈ R
- tan-1x + cot-1x = π/2, when x ∈ R
- tan-1(tan x) = x, only when x ∈ R – {x : x = (2n + 1) (π/2), where n ∈ Z}
- i.e., tan-1(tan x) = x only when x is NOT an odd multiple of π/2. Or else, tan-1(tan x) is not defined.
Arctan vs. Other Inverse Trigonometric Functions
There are a few other inverse trigonometric functions apart from arctan. All of them are listed below along with their explanation and how they differ from the arctan function:
- Arcsine Function: The arcsine is the opposite or the inverse of the sin function. It is represented as sin^-1 and has a range of -π/2 ≤ y ≤ π/2. It is especially used in situations where right angles or right-angled triangles are taken into consideration.
- Arccosine Function: The arccosine is the opposite or the inverse of the cosine function. It is represented as cosine^-1 and has a range of 0 ≤ y ≤ π. It is especially used in situations where you need to find the angle given the cosine of that angle.
- Arccotangent Function: The arccotangent is the opposite or the inverse of the cotangent function. It is represented as cotangent^-1 and has a range of 0 < y < π. It is especially used in situations where you need to find the angle given the cotangent of that angle.
The arctan function is specifically used in the following situations:
- The arctan formula can be used to create compelling effects and animations in computer graphics.
- Robotics and AI also use the arctan function to carry out various technologically advanced procedures.
- Engineering uses the arctan function to build safe and robust structures, ensure a stable supply of power, etc., in different fields of engineering.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The inverse of the tangent function in geometry is known as the arctangent formula. It is represented as arctan (x) or tan^-1 (x).
- The range of the arctangent formula is from -π/2 to π/2, or from -90 degrees to 90 degrees in other words.
- The domain of the arctangent formula is -∞ < x < ∞.
- The arctangent formula has various uses in an array of fields like engineering, robotics, AI, etc.
Quiz
Question comes here
Frequently Asked Questions
Arctan formula is used to solve problems that include right angles or right-angled triangles, or when the tangent of an angle is known and we need to find the inverse of that function.
The arctan formula is used to solve problems in various fields like engineering, physics, robotics, computer graphics, AI, and more.
The arctan function is used to compute the angle whose tangent is given. The arctan function has several identities and properties which determine its unique characteristics.
Just like the other inverse trigonometric function, the arctan function is used to compute the opposite function of an angle whose tangent is given.
Some specific properties of the arctan function that can help ease up calculations are tan (arctan (x)) = x and arctan(-x) = -arctan (x).