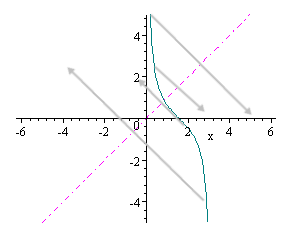Unlocking the Arccot Formula: Understanding Cotangent Inverses
Comprehensive Definition, Description, Examples & Rules
Introduction to Arccot Formula
The inverse function of the cotangent, denoted as arccot(x), is used to find the angle whose cotangent value is equal to x. By inputting a value for x, we can determine the corresponding angle. This formula is important in various trigonometry calculations.
Arccot Formula Importance in Trigonometry:
- Accrot is important in trigonometric calculation, and it is essential to calculate an angle according to its trigonometric ratios.
- Trigonometric ratios are connected with the engineering and navigation systems, which helps.
- The trigonometric function uses the arccot formula and produces the arc length, which is important to calculate and obtain a value.
Arccot Formula Importance in Mathematics:
- The formula function is very effective in mathematics as it helps to convert the binary numbers into internal storage and then calculates the inverse function’s exact value.
- Trigonometry has a great role in mathematics, and using the formula function helps to calculate a diversified mathematics calculation.
Understanding the Cotangent Function
The cotangent (cot) function is one of the six trigonometric functions and is known to be the reciprocal of the tangent (tan) function. The value of the cotangent of a particular angle is the length of the side adjacent to the angle divided by the total length of the opposite side.
The cotangent is important in trigonometry as it is one of the primary trigonometric ratios and focuses on the right angle equal to the ratio of the adjacent side to the side opposite the given angle.
What is Arccotangent (Arccot)?
The Arccotangent or the Arccot is the inverse function of the cotangent in the trigonometric formula. It can be defined as the angle with a cotangent equal to a given number or the arc of the Arccot angle.
The notation of the Arccotangent function is:
cot^(-1)
Here, it is the inverse of the cotangent function and can be expressed in this way where the domain and the range of the Arccotangent are:
-∞ < x < ∞
Arccotangent Formula
The Arccotangent formula that you can use for the trigonometric calculations is:
arccot(x) = arctan(1/x)
If you broadly were to define the formula, then it would be:
- Cotangent = Base / Perpendicular
Each of the trigonometric function has a particular inverse, and the inverse of all the trigonometric formulas are:
- inverse sine (or) arcsine
- inverse cosine (or) arccos
- inverse tangent (or) arctan
- inverse secant (or) arcsec
- inverse cosecant (or) arccsc
- inverse cotangent (or) arccot
Finding the Angle Using Arccotangent
The step-by-step instructions on how to use the Arccot formula to find an angle are:
- First, you must determine the inverse of the trigonometric function you are following.
- Determine the inverse of the cotangent of the sum.
- Use the mentioned formula appropriately, and do not make mistakes.
Example:
Find the Angle of the Triangle if the base of the angle A is one and the perpendicular side is √3.
Solution:
cot-1 (1/√3) = A
cot A = 1/√3
cot A = 60°
So, the angle A is 60°
Practical Applications
In real-world applications, there are areas where you can use the Arccotangent formula. These are:
- Physics: In physics, trigonometry is important as many mathematical calculations are done, and most utilise trigonometric calculations of the Arccot formula. There have been various theories by famous physicians that use the trigonometric formula of the tangent and the inverse cotangents.
- Engineering: It is another field that requires a lot of calculations, and you need to use trigonometric formulas, which will help you to calculate and find out the exact value. Civil engineers use this function to calculate a particular angle to build something.
- Navigation: Navigating requires a lot of calculation of the tangent and the cotangent as it will help you to find the exact angle at which the travelling has to be done, especially ships use a trigonometric calculation to understand where to move in the waters.
Scenarios where finding angles is essential are:
- Construction of a building or a house.
- While sketching or creating an art piece, the artists have to use the formula of angle measurement.
- Angle measurements are done while creating parking spaces so everything is clear.
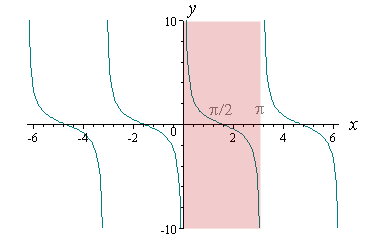
Graphical Representation
The graph is y = cot x
We choose the portion from x = 0 to x = π and reflect it in the line y = x as:
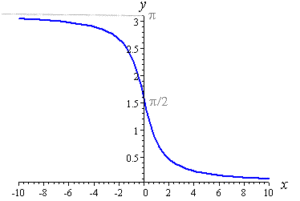
Reflection in the line y = x gives us the inverse function, and we have obtained the graph of y = arccot x as:
We can see the domain of y = arccot x is:
All values of x
And the range of arccot x is:
0 < arccot x < π
Arccotangent Identities
The common property of an arccotangent is that it is the inverse of a cotangent that belongs to the set of real numbers. So, the domain of this particular function is a set of real numbers that start from – infinity to + infinity. The common identities of the arccotangent with its formula are:
- sin(arcctg x) = 1/√(1 + x²) (X is -∞ < x < ∞)
- cos(arcctg x) = x/ √ (1 + x²) (X is -∞ < x < ∞)
- tg(arcctg x) = 1/x (X is -∞ < x < ∞)
- ctg(arcctg x) = x (X is -∞ < x < ∞)
Arccotangent vs. Other Inverse Trigonometric Functions
You can differentiate between the arccot and the arctan by the basic change in the inverse function and the formula. The arccot is the inverse function of the cotangent, while the arctan is the inverse function of the tangent.
Arccot is the inverse function of the cotangent, while arsine is known to be the inverse function of the cosine. Both of these are different, and they can be differently denoted with separate formulas.
The arccos is the angle whose cosine corresponds to a given value, yielding the principal value of the cosine. The main distinction between the arcot and arccos lies in their definitions. Unlike the arccotangent, which represents the inverse of the cotangent, with an argument equal to cotan.
You will use the Arccot Formula when the angle you want to calculate is the cotangent function, and the inverse function is cotan.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Arccot Formula is the inverse function of the cotangent.
- Physicians and civil engineers primarily use it.
- The inverse function differs for each trigonometric formula, and there is a different formula for calculating all the inverse functions.
- There is a basic relationship among all the inverse functions of the trigonometric formulas.
Quiz
Question comes here
Frequently Asked Questions
Yes, you can use all the trigonometric functions in real-life scenarios, as they all effectively function in daily life. These are:
- To find an evaluation of the sun on the ground, you can use the Arccot Formula.
- Civil engineers used to calculate inverse angles while using the formula function.
The problem is:
If x = cot-1 (- √3/3), what is the value of x?
Solution:
We know that cot2π/3 = -√3/3
x = cot-1(cot 2π/3)
So, x = 2π/3 = 120°
The function can output a real number except zero, corresponding to angles from 0 to π. Determining the range of the function is crucial for finding both the exact angle value and the variable value mentioned in the question.
The relationship of Arccot with the other trigonometric functions is: When it comes to trigonometric functions, there are a few key things to keep in mind. Arctan is the inverse function of tangent, while Arccot is the inverse function of cotangent. As Arccos functions as the inverse of cosine, and Arccosec serves as the inverse of secant. Lastly, Arsine acts as the inverse function for sine.
The properties and identities of the trigonometric functions are:
- inverse sine (or) arcsine
- inverse cosine (or) arccos
- inverse tangent (or) arctan
- inverse secant (or) arcsec
- inverse cosecant (or) arccsc
- inverse cotangent (or) arccot