Unlocking the Secrets of Isosceles Triangle Area
Comprehensive Definition, Description, Examples & Rules
Introduction to Isosceles Triangles
A triangle which has two sides equal in length and the third side with a different length is called an isosceles triangle. The angles opposite the two equal sides are also equal, or congruent.
The two equal sides are called legs and the third unequal side is known as the base. The angle between the two equal sides is known as the vertex angle, the altitude from which bisects the base, and creates two congruent right angles. Hence, isosceles triangles have symmetrical sides and angles, congruent base angles, and an axis of symmetry along the altitude.
Understanding Isosceles Triangles
A triangle with two sides of equal length and a third side with a different length is what we know as an isosceles triangle. This unique arrangement leads to various specific features and applications of isosceles triangles. For example, the angles opposite the equal sides are congruent, i.e. they have the same measure. The third angle that is between the two equal sides is called the vertex angle, which represents an axis of symmetry through the altitude drawn from it to the base of the triangle. The triangle gets divided into two congruent triangles by altitude.
The Isosceles Triangle Area Formula
The isosceles triangle area (A) is given as:
A= (½) * b* h
Here is the respective meaning of all the entities used in the given formula:
- A: Refers to the area of an isosceles triangle.
- b: Represents the base of the isosceles triangle or the third side which is of a different length than that of the two equal sides.
- h: Represents the height of the isosceles triangle or the length of the line segment that connects the vertex of the isosceles triangle at right angles to the base.
Finding the Area of an Isosceles Triangle
Here is a step-by-step procedure of measures to take when finding the area of an isosceles triangle:
Step 1: Know the Formula
The isosceles triangle area formula is given as, A=½ * b* h (where ‘A’ refers to the area of the triangle, ‘b’ refers to the base, and ‘h’ refers to the height of the triangle).
Step 2: Put in the Values
Substitute all the given values into this formula.
Step 3: Perform the Calculation
Once you know all the values for different components of the formula, perform the final calculation to compute the total area of an isosceles triangle.
Here are some numerical examples to help you understand better:
Example 1
Calculate the area of an isosceles triangle with a height of 10 cm and a base of 5 cm.
Solution
Given the above information, the area of isosceles triangle can be calculated as:
A=½ * b* h
A= ½ * 5 * 10
A= ½ * 50
A= 25
Hence, 25cm^2 is the area.
Example 2
What is the height of an isosceles triangle which is 60 cm^2 and a base of 30 cm?
Solution
Using the isosceles triangle formula, the area of the triangle can be calculated as:
A=½ * b* h
60= ½ * 30 * h
Transposing the values,
60/30=½ *h
2=½ * h
h= 4
Hence, 4 cm is the length of the height of the triangle.
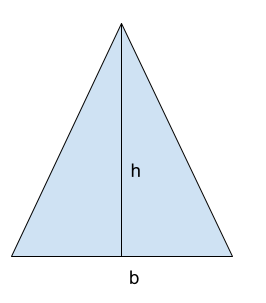
Infographics: Visual Representation
Here is a visual representation to demonstrate the formula and the concept of isosceles triangle area:
In the above isosceles triangle, ‘b’ refers to the base, and ‘h’ refers to the height of the triangle.
Now, the area ‘A’, can be calculated as, A=½ * b* h
Substitute all the values available to you into this formula and perform the final calculation to compute the total area of an isosceles triangle.
Special Cases: Equilateral Triangles
Equilateral triangles are special kinds of isosceles triangles in which the base is also of the same length as the two equal sides. In other words, all the sides of an equilateral triangle are equal. This also means that all the angles in an equilateral triangle are of equal measure and are 60 degrees each. To calculate the area of an equilateral triangle, we use a particular formula due to its unique properties:
A= √3/4 * s^2
Here is a detailed explanation of all the components in the given formula:
- ‘A’ denotes the area of the triangle.
- ‘s’ refers to the length of the equal sides of the triangle, which is squares and multiplied by √3/4 to compute the total area of an equilateral triangle.
Real-World Applications
Isosceles triangles are used in a variety of real-life applications like:
- Architecture: In architecture, isosceles triangles come in handy in various processes like designing roofs that are triangular in shape, windows, and other triangular decorative elements in any kind of space.
- Engineering: Isosceles triangles are used for a variety of processes in engineering like operating truss systems where they act as the crucial elements that bear weight. Isosceles triangles are also used in the mapping of land and measuring irregular pieces of land.
- Art: apart from the above-given processes, isosceles triangles also have a useful role to play in the aesthetic and creative field. In art, they are used to create aesthetic geometric shapes and also carry out perspective drawing to include realistic proportions in the artwork.
Comparing Isosceles Triangles with Other Triangles
The area of any triangle depends on its base and height. Here is a representation of the different formulas used to compute the area of different triangles:
Isosceles Triangle (has two sides equal in length and one different in length)
An isosceles triangle’s area can be computed using the formula:
A=½ * b* h
(where ‘A’ refers to the area of the triangle, ‘b’ refers to the base, and ‘h’ refers to the height of the triangle).
Scalene Triangle
A scalene triangle’s (has all sides with a unique length) area can be computed using the formula:
A=½ * b* h
(where ‘A’: is the triangle’s area, ‘b’: is the triangle’s base, and ‘h’: is the triangle’s area).
Equilateral Triangle
An equilateral triangle’s (has all sides equal in length) area can be computed using the formula:
A= √3/4 * s^2
(where ‘A’: is the area of the triangle and ‘s’: is the length of the equal sides of the triangle)
Common Mistakes and Pitfalls
Here is a list of some common errors people make while computing the area of an isosceles triangle and how you should avoid them:
- Using the incorrect formula: Keep in mind that due to their distinct qualities, triangles have different formulas for calculating their areas, so you should always use that method to get the area of a given triangle.
- Disorienting the terms base, legs, and height: Always keep in mind that the base of the triangle is the side that is shorter than the other two equal sides, and the height is the perpendicular distance from the vertex (the angle between the two equal sides) to the base of the triangle. The formula does not apply to the legs, which are an isosceles triangle’s two equal sides. Be careful not to mix up the components that are provided.
- Forgetting to Divide by Two: To determine the precise area of an isosceles triangle, always remember to divide the whole product by 2.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A triangle with two sides of equal length and a third side with a different length is what we know as an isosceles triangle.
- The angles opposite the equal sides in an isosceles triangle are congruent, i.e. they have the same measure.
- The third angle in an isosceles triangle that is between the two equal sides is called the vertex angle, which represents an axis of symmetry through the altitude drawn from it to the base of the triangle. This altitude divides the triangle into two congruent right triangles.
- The area of an isosceles triangle (A) can be represented as A=½ * b* h (where ‘A’ refers to the area of the triangle, ‘b’ refers to the base and ‘h’ refers to the height of the triangle).
Quiz
Question comes here
Frequently Asked Questions
The area of an isosceles triangle takes only the base or the unequal side into consideration, the area of a scalene triangle takes only the side that acts as the base into consideration, and the area of an equilateral triangle can consider any side as all the sides are of equal length.
An equilateral triangle has all sides and angles equal in length and measure. Unlike an isosceles triangle’s area formula that takes the base and height of the triangle into consideration, the area formula of an equilateral triangle considers any side of the triangle to compute the total area.
Isosceles triangles can be used in architecture to create triangular windows and roofs and in engineering to design maps of land, truss systems, etc.
To calculate the area of an isosceles triangle accurately, remember to use the right formula, not confuse base, legs, and height, and not forget to halve the final product of base and height.
Yes, an isosceles triangle has two equal sides, two equal angles, and an axis of symmetry along the altitude. These properties greatly affect its area calculations.