Understanding the Cosecant Formula in Trigonometry
Comprehensive Definition, Description, Examples & Rules
If you want to develop your understanding on the concept of trigonometry then you are at the right page. You will get to know about the formulas, practical examples, graph presentation and most important is use of cosecant in daily life. You will also get a chance to improve your understanding through the worksheet that is given in the end at this page.
Brief about Concept
Trigonometry is a basic concept of mathematics that gives an insight to the students about the calculation of the angle. These concepts are useful in various domains like science and so on.
Trigonometry and its relevance in mathematics
Trigonometry contains sine, cos, and tan as a basic concept. Its reciprocal is cosecant, secant, and cot. These concepts are important in the field of mathematics to understand the right angle triangle.
The trigonometric functions and their significance
- These concepts are useful in calculating Algebra, geometry, and various other equations related to the right-angle triangle.
- Trigonometry is useful in various domains, including science, distance, architecture, and so on.
Define the Cosecant Function?
Cosecant is a part of the trigonometry concept. It is the reciprocal of sinθ. It is represented like:
- Cosecθ = 1/ sinθ
Define the cosecant (CSC) function and its relationship to other trigonometric functions.
Cosec has a relationship with the sine. It is reciprocal of sinθ and referred to as 1/sinθ, and the sinθ is reciprocal of cosec.
Explain how the cosecant function is used in trigonometry and real-world applications.
- These concepts are relevant in the trigonometry.
- In the real world, these formulas are useful in domains like physics, astronomy, and so on.
- You can solve any Complex equation of trigonometry by the use of the Cosecant formula.
The Cosecant Formula:
Cosecant is the reciprocal of sine. You can explain this concept easily by developing your understanding.
Present the cosecant formula, which defines the cosecant of an angle in a right triangle.
In the right-angle triangle, the formula for cosecant is a division of opposite angle/hypotenuse.
Cosec θ = 1/sinθ
Explain how the cosecant formula is derived from the sine function.
You must know the sin θ formula to derive the cosecant formula. Sinθ refer as
adjacent side / hypotenuse
You need to take the reciprocal of this to find the cosecant that is 1 / sinθ
You will get the hypotenuse/ adjacent side through its reciprocal.
Applications of the Cosecant Formula
Cosecant is reciprocal of sinθ. It has wide use in the fields like science, physics, and so on.
Discuss how the Cosecant formula is applied in solving trigonometric problems.
- You can solve the equation related to the sine and cos through cosecant.
- You can find the solution of trigonometry expression like (sin²θ+ cos²θ)=1. You can also refer to this as cosec²θ =1+cot²θ.
Include examples of real-world situations where the Cosecant formula is useful, such as in physics and engineering.
In the real world, this concept is practically used in various domains,
- In physics, it is used for calculating angular shape and distance.
- Engineers use this concept for calculating amplitude.
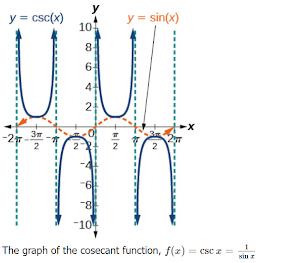
Graphical Representation of the Cosecant Function:
The properties of the cosecant graph.
The graphical presentation includes asymptotes and periodicity.
- Amplitude are positive and negative values like (2 and -2)
- Asymptotes can be seen on the vertical side.
How to Calculate Cosecant Values
If you want to calculate the cosecant value, then you have to do the reciprocal of the cosecant.
Explain how to calculate cosecant values for specific angles.
- First, you should know the value of the angle to calculate cosecθ.
- You should know the trigonometry chart that includes the value for sinθ. For example, if θ is 30⁰, then it would be ½ for sin30⁰.
- You should apply this cosecant formula that is reciprocal of 1/ sinθ.
- Cosec30⁰ = 1/sin, which means 1/0.5 would be 2.
Provide step-by-step instructions on using the cosecant formula to find cosecant values
If you want to calculate the cosec 45⁰, then you need to follow these steps:
- You should know the angle that is 45 in this case.
- You need to use a cosec formula that is 1/sin θ.
- Cosecθ = 1/0.70
- Cosec45⁰ would be 1.41
Inverse Cosecant Function:
These functions refer to cosec-¹. It reverses the trigonometric functions.
Introduce the concept of the inverse cosecant function (arcsec or csc^(-1)).
Inverse cosecants are inverse of cosec function.
It is refer as :
y = cosec-1x (arccosecant x)
Cosecθ = x.
Explain how to use the inverse cosecant function to find angle measures.
- You can use these functions in determining the cosecant value. You measure the angle by using this concept.
- Assume that you have x =2, and now you have to find the value of θ then cosecθ=2, and you will find cosec-¹ (2)
Trigonometric Identities Involving Cosecant
Trigonometry formulas are related to each other. Cosec is significant concept in trigonometry. If you want to know it’s functioning, then you can observe it in the next section.
Present common trigonometric identities that involve the cosecant function
Cosecant is a reciprocal of sineθ. You can see its relation with sine-like:
- Cosecθ =1/sinθ
- Sinθ = 1/cosecθ
You can solve any equation related to the cosec and sine.
Discuss how these identities can simplify trigonometric expressions.
There are various identities that carry trigonometric expressions.
- In Pythagoras, these expressions are :
sin²θ + cos²θ=1
Cosec²θ – cot²θ=1
- Other expression like ratio in trigonometry with cosecant can be expressed as :
Cosecθ=1/sinθ
There are various other identities as well that carry this trigonometric expression.
Practical Examples and Problem Solving
This trigonometric concept has wide relevance at the present time. It can be used in multiple domains spe, specifically in science.
Include worked examples that demonstrate the application of the Cosecant formula in solving trigonometric problems.
For example, cosecθ=2, then you need to find the value of θ here.
- Cosecθ=1/sinθ
- Then, you need to take the reciprocal of 2, which would be ½ sin θ.
- You must know the value of ½ for sin, which is 30⁰.
So, in this example, the angle is 30⁰.
Cosecant Formula in the Unit Circle
Cosec is also related to the unit Circle, and you will find a relationship between both of them.
Explain how the cosecant formula is related to the unit circle and the geometric interpretation of trigonometric functions.
Unit circle has a radius of 1 unit that contains an origin point that we refer to as O.
The cosecant function is 1/sinθ.
You can find the graphical representation and its relation with cosecant.
- Cosec=1/sinθ.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- These concepts are important in the field of mathematics to understand the right angle triangle.
- The Formula for cosecant is a division of opposite angle/hypotenuse.
Cosec θ = 1/sinθ - Cosecant is a part of the trigonometry concept. It is the reciprocal of sinθ.
- In the real world, these formulas are useful in domains like physics, astronomy, and so on. You can solve any Complex equation of trigonometry by the use of the Cosecant formula.
- Its representation is related to the asymptotes and periodicity.
- Students generally commit mistakes by ignoring the trigonometry table or the value of angles in trigonometry. All the expressions like cosec and sine are related to each other, and if you forget the angle digit, then you might face problems in solving such an equation.
- You can practise on the worksheet provided by Edulyte for a better understanding of this concept.
Quiz
Question comes here
Frequently Asked Questions
Cosecant is the reciprocal of sinθ, and sin is also connected with cosec. That’s how cosecant has a link with the sine function.
It can be graphed by understanding amplitude and other factors.
You can calculate the cosecant value for angles like cosecθ, which is the reciprocal of sin θ.
There are various trigonometric identities like:
- Cosecθ =1/sinθ
- Sinθ = 1/cosecθ
In Pythagoras, these expressions are: sin²θ + cos²θ=1 Cosec²θ – cot²θ=1 Other expressions like ratio in trigonometry with cosecant can be expressed as Cosecθ=1/sinθ
Unit circle has a radius of 1 unit that contains an origin point that we refer to as O. In the unit circle, you can find the angle of the cosecant corresponding to the line segment from the origin of the circle. The cosecant function is 1/sinθ. You can find the graphical representation and its relation with cosecant Cosec=1/sinθ.