Mastering the Cosecant and Cotangent Formulas: Trigonometric Essentials
Comprehensive Definition, Description, Examples & Rules
Introduction
Cosec and Cotangent are important concepts in trigonometry. Their formulas are the reciprocals of sine and tangent, respectively. Understanding these concepts helps calculate distances. This page will provide you with information about the cosec cot formula.
A brief overview of the importance of the Cosecant (cosec) and Cotangent (Cot) functions in trigonometry.
- Cosec and Cot are the reciprocals of sine and tangent in trigonometric functions.
- The cosecant is a mathematical term used to describe the reciprocal of the sine. It represents the ratio of the hypotenuse to the side opposite an angle in a right-angle triangle.
- Cosecant is written as cosec θ, where (θ) is the angle.
- The Cotangent is opposite to the tangent, referring to the base ratio and the right angle’s perpendicular ratio.
- It is reflected as cotθ, where (θ) is an angle.
Both concepts are significant in the properties of triangles. You can solve the trigonometric equations by using these concepts.
Understanding Cosecant (cosec)
Cosecant, often referred to as cosec, is the reciprocal of sine. It has important applications in trigonometry, particularly when working with right-angled triangles and determining their properties.
Definition and explanation of the cosecant function
Cosec is one of the trigonometric functions. It is reflected as cosecθ. Coscent is just the opposite of sine.
Cosecθ = adjacent / hypotenuse
Cosecθ has a reciprocal relationship with the sine.
How to calculate cosec using the reciprocal of the sine function
You can find out the value of cosθ by simply using the reciprocal of sine.
Cosθ is equal to 1/sinθ.
- You must consider the angle that is referred to as θ.
- You should know the sinθ, and then you need to do it reciprocally to find the cosecθ.
Practical examples illustrating the use of cosec
- You can calculate the amplitude and periods using the coscent formula.
- It is also useful in various domains like astronomy, navigation, architecture, ultrasound, and so on.
- It is also useful in domains like physics and engineering.
Understanding Cotangent (Cot)
Cotangent is just the opposite tangent, and it is reciprocal of tan. It is referred to as cotθ.
Definition and explanation of the cotangent function
A cotangent is one of the trigonometric functions. That is useful in solving trigonometric equations.
Cotθ = 1/tanθ
Cotangent is the reciprocal of tangent, where θ is the angle.
How to calculate Cot using the reciprocal of the tangent function
The formula for Cot is just the reciprocal of the tangent.
Cotθ = 1/tanθ
- You must consider the angle that is referred to as θ.
- You should know the sinθ, and then you need to do it reciprocally to find the cosθ.
Real-world scenarios where Cotangent is applied
- You can calculate the right angle by using the coscent formula.
- It is practically used in domains like physics and engineering.
- It is also useful in various domains like astronomy, navigation, architecture, ultrasound, and so on.
- In computer graphics, the use of Cotangent is significant.
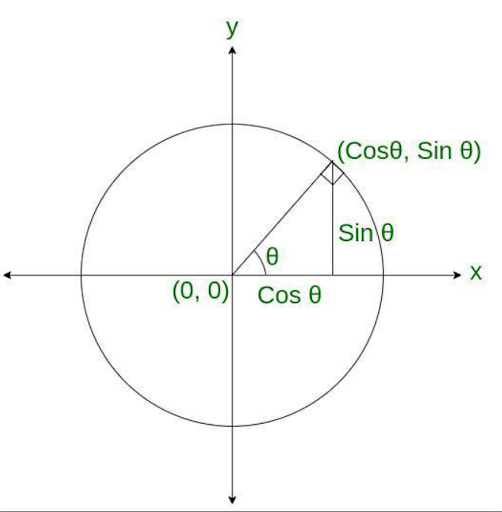
Unit Circle Representation
You can find out the relationship between trigonometry by using unit circle relationships.
Visual representation of the unit circle to understand the relationships between sine, cosine, Cosecant, and Cotangent
- You need to draw a circle with a point ‘o’ that is the origin centre.
- You must use the x-axis on the right and the y-axis on the left.
- The Y axis coordinates the sine θ.
- You can calculate cosecθ and cotθ as the reciprocals of sinθ and tanθ.
All these angles are related to each other.
Cosecant and Cotangent Identities
Cosecant and Cotangent are significant concepts in trigonometry and one of the functions.
Introduction to key identities involving cosec and Cot, such as their relationships with sine, cosine, and tangent
- Cosecants are just the reciprocal of sin, which is referred to as 1/sin.
- In Pythagoras, you can reflect it as cosec2 = 1 + cot2 θ.
You can use this concept in physics and engineering. This concept is also useful in geometry.
- Cotangents are reciprocals of tangents that are referred to as cotθ = 1/tanθ.
- In Pythagoras, you can express this as cot² = 1 + cosec² θ.
Cosec cot formula is (cosec θ – cot θ)2 = (1 – cos θ)/(1 + cos θ).
This concept is useful in engineering, physics, and other domains like surveying and so on.
Graphical Representations
You can get better insights about these topics through the graphical representation.
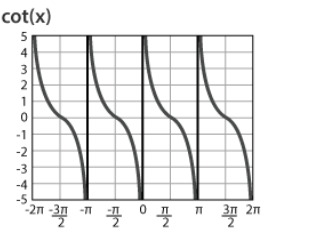
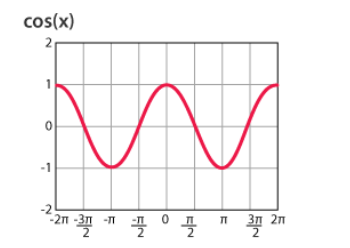
Graphs illustrating the graphs of the cosecant and cotangent functions
- The cosecant function is periodic, with 2π units at the x-axis.
- In Cotangent, the π can be repeated.
- Vertical asymptotes and amplitude are also part of the graph that gives a proper idea about the relation of the trigonometry concept.
Trigonometric Equations Involving Cosecant and Cotangent
- Find the value of cos θ with respect to the triangle, such that the sides opposite and adjacent to θ measure six units and eight units, respectively.
To find cos θ, we need the adjacent side and the hypotenuse.
Here, the adjacent side is 8.
But we are not given the hypotenuse.
To find this, we use the Pythagoras theorem:
hypotenuse = opposite + adjacent
= 6² + 8²
= 100
hypotenuse = √100 = 10
Therefore, cos θ = adjacent/hypotenuse = 8/10 = 4/5.
cos θ = ⅘
- Find the Cotangent of x if sin x = 3/5 and cos x = -4/5 using the cotangent formula.
Solution:
We know that cot x = (cos x) / (sin x).
= (-4/5) / (3/5)
= -4/3
Answer: Cot x = -4/3.
Applications in Real Life
- These concepts are useful in wide domains, like physics and engineering.
- Whether it is data management or triangle properties, Trigonometry plays a significant role.
Practical applications of Cosecant and Cotangent in fields like physics, engineering, and astronomy
- Cosecant and cotangent concepts are useful in physics for mechanical systems. For example, engineers use cotangent formulas for measuring the angle of a car.
- The cotangent concept is used for the study of angles and their velocity measurements. For example, you can find the wheel speed by measuring the angle tangent.
- You can measure the altitude of celestial bodies by using the cosecant and contingent formulas.
Common Mistakes and Pitfalls
Highlighting common errors and misconceptions when working with COS and COT functions
- Students frequently forget the Cosecant and tangent.
Mistake avoiding ways : It is necessary for students to remember that cosec is the reciprocal of sineθ and cotθ is the reciprocal of tangent.
- Students forgot the use of θ while solving the equation, which can impact their answers.
Mistake avoiding ways: In order to avoid such mistakes, it is necessary for students to remember the use of θ while solving equations.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Both have relevance, and these concepts are useful in finding the distance.
- Cosec and Cot also refer to the reciprocals of trigonometric functions.
- Cotθ = 1/tanθ is the formula for cotangent.
- Cosθ = 1/sinθ is the formula for coscent.
- Both concepts are useful in the physics and engineering domains. Whether it’s astrology or a survey, Whenever there is a measurement of the right angle, the cosecant and tangent become significant.
- You can improve your trigonometry concept by practicing through Edulyte’s worksheet.
Quiz
Question comes here
Frequently Asked Questions
You can calculate cosθ by using its formula, 1/sinθ.
Cosecant is the reciprocal of sine, and Cotangent is the reciprocal of tangent, which makes a connection between all three of them.
The identities involved in Cosecant and Cotangent are as follows:
Cosecθ =1/sin
Cotθ=1/tan
- Find θ in cosθ=2.
You need to know its reciprocal, which is ½, and then you must remember the sinθ value for ½. After that, you will find the cosecent value as 5π /6.
- While finding the value for cotθ = √ 3,
You have to do a reciprocal of √ 3, which would be 1/√ 3. After putting in the value, you will find the answer of 5π /6.