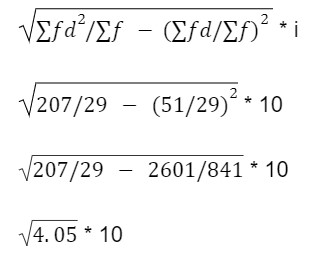Deviation Demystified: Unraveling Averages, Means, and Standard Deviations
Comprehensive Definition, Description, Examples & Rules
Understanding Average Deviation and Mean Deviation
Both average deviation and mean deviation are an essential part of mathematical calculations. The average deviation is calculated while computing the mean and then the distance between every score and the mean without regard to whether the score is below or above the mean. The average deviation is also known as the average absolute deviation.
Mean deviation is a statistical measure that you use to calculate the average deviation from the mean value from a given data set. You use the mean deviation to calculate the average absolute difference between the data provided to you.
Significance in Statistics and Data Analysis
The significance of both average and main deviation in statistics and data analysis, include:
- It helps to calculate the central value in the distribution.
- You use the deviation values to signify that the data points are far from the mean.
- The difference in the range is higher than both the deviations.
- It simplifies the calculation of measurements when there is distributed data.
How to Calculate Average Deviation?
The step-by-step procedure you can follow while collecting average deviation includes:
- First, you must calculate the mean of all data points.
- Then, find the difference between each of the data points and the mean.
- Finally, calculate the average of all the absolute values of the differences.
Examples:
How to find Average Deviation for the given data: 2,4,6,8,10?
Solution:
n = 5
x= (2+4+6+8+10)/5
x ,= 6
Average Deviation is
(|2 – 6| + |4 – 6| + |6 – 6| + |8 – 6| + |10 – 6|) / 5
(4 + 2 + 0 + 2 + 4)/ 5
2.4
So,
The average Deviation is 2.40
Calculating Mean Deviation: Step-by-Step
The step-by-step guide that you can go through which will help you to find out the mean deviation is:
- Calculate the mean value for a particular data.
- Subtract the mean from every data value, which will help you find the absolute deviation.
- You need to find the mean of the absolute deviation to get the mean deviation value.
Examples:
How to find Mean Deviation using Mean and Standard Deviation?
Classes | Frequencies |
20-40 | 3 |
40-80 | 6 |
80-100 | 20 |
Solution:
c | f | m | X−A(60) | |d| | f|d| | d = (x-a)/t | fd | d2 | fd2 |
|---|---|---|---|---|---|---|---|---|---|
20-40 | 3 | 30 | -30 | 30 | 90 | -3 | -9 | 9 | 27 |
40-80 | 6 | 60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
80-100 | 20 | 90 | 30 | 60 | 1200 | 3 | 60 | 9 | 180 |
∑f=29 | ∑f|d|= 1290 | ∑fd = 51 | ∑fd2 = 207 |
x= A + ∑fd /∑f *i
60+ 51/29*10
7.76
MDX = ∑f|d|/∑f
1290/29
44.48
Deviation is:
20.12
So, Mean deviation is 20.12.
The Average Deviation Formula
The mathematical average deviation formula that you should use will help you to calculate is:
- 1/n Σ | xi – x |
If you want to describe the formula, then it will be:
xi is the data values that are given in a particular set
x is the mean of the set
n here is the total number of data values that are present in the sum.
The Mean Deviation Formula
The mathematical mean deviation formula you use for calculating is:
Grouped Data: (Σ1n | xi – x | )/(Σ1nfi)
Defining the formula for mean deviation:
fi here is the repetition frequency of xi.
xi denotes the middle value of the class interval.
Practical Examples: Finding Average and Mean Deviation
The real-world examples of applications where you use both average and main deviation are:
- Both these deviations have a significant role to play while calculating business and commerce performance, and companies also use them to understand the performance of their marketing strategies.
- One of the primary areas where the deviation is used is to calculate the percentage of marks, and the student’s performance is compared with the other students by making an average.
- The company wants to do a graphical analysis of data values and data sets and use this raw data to understand their performance.
Showing how these measures provide proper insights into data:
- These measures provide proper insights into data and represent the typical value, which is essential for observation.
- One of the primary insights that the data provide is showing how the company’s performance is then how well the employees perform.
Comparing Average Deviation and Mean Deviation
Differences
Average deviation and mean deviation have a basic difference where the mean deviation is a statistical measure that helps you to compute the average deviation from an average value of a data collection. On the other hand, the average deviation is the calculation of the mean from a particular distance.
Similarities
The primary similarity between an average and a mean deviation is that both measure the numerical data and help you find out the data sets’ lowest and highest values and the data group’s middle term.
The average deviation is considered a better major, which comes with absolute variability, but when you need to determine the size of the data and the data group has a lot of values, then using the mean variation might be helpful.
Interpreting Average and Mean Deviation
The significance of calculating the deviations is:
- It shows how much variation comes from the main group.
- The higher the deviation values, the more significant the data point will be from the mean.
- You can identify the central value of the distribution.
- You can do an indicated research among the data values that are provided to you among the data set.
To indicate the data in the form of a data analysis you need to keep a few things in mind:
- A division close to zero indicates that data points are much closer to the mean.
- If you have a large deviation, it will indicate that the data sets are spread far away from the mean.
If you keep this data in mind, you can format it in the form of data analysis and the following data sets to represent the values.
Average and Mean Deviation in Descriptive Statistics
The average and mean deviation are important. In descriptive statistics, these divisions are known to be individual data points from which the mean is calculated, and the data sets are highly crusted around the mean.
Roles in Summarizing and Analyzing
The role of average and mean deviation in summarizing and analyzing includes:
- It has a primary role in summarizing, analyzing, and representing the data sets’ data.
- You can derive the data in tables and graphs, which involves measuring Central tendency.
- You can use the measure of dispersion or variance, which will help you represent the data sets using average and mean deviation.
Standard Deviation Formula for Ungrouped Data
The standard deviation formula for ungrouped data Ungrouped Data includes:
(Σ1n | xi – x | )/n
Defining the formula:
xi is the ith observation of the group.
x is representing the central, whether it is the mean mode or median.
n is the total number of observations present in the group.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Calculation with the average and the mean deviation is challenging enough compared to the other dispersion.
- Giving more way to the extreme values and less to the main ones is important while calculating the deviation.
- Calculating the mean and average deviation in open intervals is impossible.
- Using average and mean deviation when two or more data sets are provided is impossible.
Quiz
Question comes here
Frequently Asked Questions
Practical examples where you can use standard deviation for calculating the ungrouped data include:
- Calculating weather forecasting.
- Calculating the performance of stock in real estate.
- It also helps calculate medicines’ performance in the healthcare department.
- In human resource management, using standard deviation is also very important to calculate the performance of employees.
The calculation for the standard deviation for ungrouped data is done with the formula:
(Σ1n | xi – x | )/n
Here,
xi is the ith observation of the group.
x is representing the central, whether it is the mean mode or median.
n is the total number of observations present in the group.
Find the Average Deviation for the given data: 5, 6,8,10,12,14
Solution:
n = 6
x= (5+6+8+10,11,14)/6
x ,= 9
Average Deviation is
(|5 – 9| + |6 – 9| + |8 – 9| + |10 – 9| + |11 – 9| + |12 – 9| ) / 6
(4 + 3 + 1+1 + 2 + 3)/ 6
2.33
So,
The average Deviation is 2.37
The limitations you should be aware of are:
- If you compare it with the other measures of dispersion, then calculation using the standard deviation is more challenging.
- You need to give more weight to the extreme values and less to the near means.
- You cannot calculate the average and the mean deviation in open intervals.
- If two or more data sets are provided, then the calculation will not be possible for comparison.
Average Deviation is calculated when you compute the mean and a particular distance between the group data without regard for whether the mean is above or below the data.
The primary difference between average and mean deviation is that average deviation calculates the mean from a particular distance. In contrast, mean deviation is a statistical measure to compute the average deviation of the average value.
Standard deviation is a broader concept, and average deviation is a part of standard deviation.