Understanding Cosine (cos θ): Formula and Calculation
Comprehensive Definition, Description, Examples & Rules
Introduction to Cosine (cos θ)
The cosine function in trigonometry is the ratio of the adjacent sides to the hypotenuse. It is an essential trigonometric function, and itself is the complement of the sine function. The significance of cosine in trigonometry is it helps us to find the exact length of the sides of the triangle irrespective of the given angles of the triangle.
Role in Geometry and Physics:
- The cosine function plays a very important role in geometry by calculating the exact length and side of the triangle and also functions as an essential economic function.
- Trigonometry is directly related to physics, and many expert physicians have used d trigonometric functions in their calculations. Newton’s theory uses most trigonometric functions to provide the essential details.
Cosine Formula
The fundamental cos theta formula that you use for calculating the cosine is
- cosθ = base/hypotenuse
Here,
The base is known to be the base of the triangle, while the hypotenuse is the side opposite to the right angle of the triangle.
If θ is one of the acute angles of the triangle, then sinθ is the ratio of the opposite side of the hypotenuse, and the cosec is the ratio of the adjacent side to the hypotenuse. The cosine directly relates to the right-angle triangle, and the calculation of cos theta is possible when the formula is used in a right-angle triangle itself.
Calculating Cosine
The step-by-step guide on calculating cos values is as follows:
- You need to determine the base and hypotenuse of your right-angled triangle.
- If one of the sides is not provided, use the right angle triangle formula to calculate the sides.
- Then, use the cos theta formula to calculate the cosine values effectively, and you will get the value you want to calculate.
- You can also use a trigonometric table or calculator, which will help you make your calculations much easier and more effective.
The trigonometric table that you can use for your calculation is:
θ | 0°(0 Radians) | 30° (π/6) | 45°(π/4) | 60° (π/3) | 90° |
sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
tan | 0 | 1/√3 | 1 | √3 | ∞ |
csc | ∞ | 2 | √2 | 2/√3 | 1 |
sec | 1 | 2/√3 | √2 | 2 | ∞ |
cot | ∞ | √3 | 1 | 1/√3 | 0 |
The Unit Circle and Cosine
If you use the unit circle, then the sign of the angle of the circle will equal the value of the endpoint on the unit of the circle where the arc length is situated, and the cosine of the angle will equal another value of the endpoint. To read the cosine value of the unit circle, the coordinate of the point where the other side of the angle will intersect is cosθ.
The behavior of the cosine function is inversely related to the angles as the ratio of the side edges of the hypotenuse will change with the regular change in the value of the angles. The cos theta formula will be different if the angle is changed, so the behavior of the cosine function inversely relates to the behavior of the angle.
Common Cosine Values
The tables to follow for the common Cosine Values of the key angles are:
θ | 0° | 30° | 45° | 60° | 90° | 120° | 180° | 270° | 360° |
cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1/2 | -1 | 0 | 1 |
For the non-standard angles, you need to follow a particular procedure to express the angles in the form of degrees and then convert the measurement of the degrees into radians by multiplying it with π/180. Converting the measurement will allow you to make accurate calculations.
Applications of Cosine
The real-world applications of cosine include:
- Engineering: Engineers have a high role in using trigonometric calculations in their work as civil engineers have to do a lot of calculations to finalize their work, and trigonometric calculations have a huge part for civil engineers in calculating and finding the perfect measurement.
- Physics: Many famous physicists use trigonometric calculations in their physical reports, especially Newton’s Law, which uses many trigonometric formulas. Cosine has a perfect role in physics, and calculation in physics becomes very important while using trigonometry.
- Navigation: The navigation process has a great role in trigonometric calculations and makes it easy to navigate and calculate latitude and longitude.
The connection between the trigonometric functions and sound wave analysis is very effective as the period vibrations can be calculated through the sine or the cosine function. The sound wave analysis is also a cosine wave where the calculation is done with the cosine formulas.
Cosine Identities and Relationship
The reciprocal identities of all the trigonometric calculations that involved cosine are:
- cosθ = 1/secθ
- secθ = 1/cosθ
The trigonometric identities are used to simplify all the complex equations that involve the trigonometric functions and are a relationship between the sides and angles of the triangle.
The basic understanding of all these trigonometric identities is that they are inversely related, and the trigonometric identities make the calculation very easy.
To define the sine and cosine relationship, the trigonometrical identity that we use are:
- cotθ = cosθ/sinθ
- tanθ = sinθ/cosθ
The Pythagorean trigonometric identity that uses the cosine is:
- sin²θ + cos²θ = 1
Calculating the Angles Using Inverse Cosine
The inverse trigonometric functions are the inverse functions of all the basic trigonometric functions like cosine or sine, and these functions are also known as cyclomatic. The inverse trigonometric functions are used to find the value of a given angle with the other trigonometry ratios. The inverse trigonometry functions have a primary application in physics and Engineering and have a good role in geometry. The inverse trigonometric functions, or Arc functions, help calculate a given value.
The inverse trigonometric function for cosine is Arccosine or Arrcos.
Example:
Using Arrcos calculate the angle of the triangle with Hypotenuse 20 base 14
Let the angle be A
So, cos A = 14.2/20 = 0.710
C = Arccos 0.710 = 45°
So, the Angle is 45°
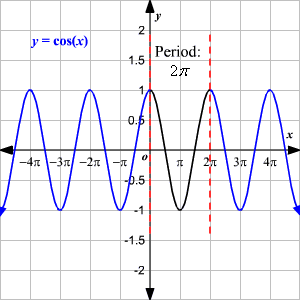
Graphing Cosine Functions
The graphical representation of the cosine function y = cos(x) is:
The periodicity and the amplitude of the cosine function involve:
The amplitude of the graph y = a cos(bx) is the number by which it varies above and below the x-axis.
The amplitude is | a |
The periodicity of the cosine function is the exact length of the shortest interval present on the x-axis.
The Periodicity is 2π/ | b |
Challenges and Advanced Topics
The advanced trigonometric concepts involving cosine are:
- Inverse Cosine Function
- Cosine Addition Formulas
- Half-angle Identities
- Angle inclination of Line
- Trigonometric Equations
One of the challenges that you have to face while using trigonometric calculation is solving the trigonometric equations, as different equations will be difficult for you to calculate, the trigonometric equations and inequalities are:
- sin θ = sin α
- cos θ = cos α
- tan θ = tan α
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The sine and the cosine functions are the most important functions that help calculate trigonometric calculations.
- The advanced topics can be challenging, so you must effectively use the initial formula to make your calculations worth it.
- All trigonometric functions are inversely related, making your calculation much more stable and effective.
Quiz
Question comes here
Frequently Asked Questions
The cos theta formula while calculating as and cosine angle is abbreviated as:
- cosθ = base/hypotenuse
Here,
The base is the base of the triangle, while the hypotenuse is the side opposite to the right angle of the triangle.
The common cosine values that you can use for your calculations are:
θ | 0° | 30° | 45° | 60° | 90° | 120° | 180° | 270° | 360° |
cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1/2 | -1 | 0 | 1 |
In situations when you have to calculate the cosine values of a non-standard angle, then you have to follow up a process that will help you to convert the non-standard angle into a proper measurement by using the radians where you have to multiply the non-standard angle with the π/180. It will help you find the approximate value of the non-standard cosine angle.
The economic identities are the ones that make your complex equations very simple and have a primary relationship with the triangle, as the identities help you to understand your equation. The mixed calculation of the equation is much easier and simpler.
The famous Pythagoras trigonometric function that you use for your cosine is:
- sin²θ + cos²θ = 1