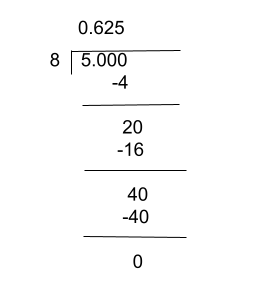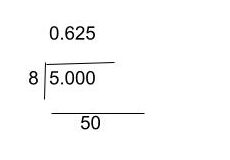Mastering Decimal Conversion :A Comprehensive Guide on Converting Fractions to Decimals
Comprehensive Definition, Description, Examples & Rules
“Convert fractions to decimals.…” how many times has this instruction left you staring blankly at the fraction? What if Edulyte tells you that there are ways in which you can overcome your fear of converting fractions to decimals? Check out this resource on handling such mathematical problems with ease.
Introduction: Significance Of Converting Fractions To Decimals
Convert ⅝ into decimals. Have you ever faced a problem demanding the converting fractions to decimals and felt fear grip your soul as you contemplate the mathematical procedure that awaits you?
Well Edulyte is here to not only get you over your fear but also master the procedure of converting fractions to decimals effortlessly!
But first, we need to understand why it is important to convert fractions into decimals.
Mathematical Operations
- Decimal numbers are often easier to work with in arithmetic operations; addition, subtraction, multiplication, and division. Converting fractions to decimals allows for seamless integration into these operations.
- Decimals provide a convenient way to compare the magnitudes of numbers. Comparing fractions directly can be complex, but converting them to decimals simplifies the process.
- In geometry and graphing, decimal numbers are commonly used to represent coordinates and measurements.
Real-World Scenarios
- In finance, decimal numbers are standard for representing currency values.
- Converting fractions to decimals is essential in fields like engineering and construction, where precise measurements are critical.
- In everyday life, especially in cooking, recipes often involve measurements in decimal form. Converting fractions to decimals is essential for accurately following recipes and adjusting ingredient quantities.
- Converting fractions to decimals is fundamental in expressing numbers in scientific notation, making it easier to work with very large or small values.
Searching for the ideal Maths assistance catering exclusively to your study needs? Sign up for free. Check out our tutors and get classes customised to your specific learning needs!
Understanding the Basics: What Are Fractions And Decimals?
Fractions:
- A fraction is a mathematical expression that represents a part of a whole. It consists of two numbers, one written above the other and separated by a horizontal line.
- The number above the line is called the numerator, and the number below the line is called the denominator. The fraction a/b represents a parts out of a whole divided into ‘b equal parts. For example, 3/4 represents three parts out of four.
Decimals:
Decimals are another way to express numbers. They are a system of representing numbers based on powers of 10. A decimal number can include a whole number part, a decimal point, and a fractional part. For example, in the decimal 2.752.75, “2” is the whole number part, and “.75” is the decimal part.
Converting Between Fractions and Decimals:
Converting between fractions and decimals involves expressing the same quantity in different forms. This conversion is essential for several reasons:
Ease of Calculation:
- Decimal numbers are often easier to work with in calculations, especially in arithmetic operations like addition, subtraction, multiplication, and division.
Comparisons:
- Decimals provide a straightforward way to compare the sizes of different quantities. Comparing fractions directly can be challenging, but converting them to decimals makes the comparison more intuitive.
Compatibility with Applications:
- Decimals are the standard representation in many real-world applications, such as finance, science, and engineering.
Graphical Representations:
- Decimals are often used in graphical representations and measurements. Converting fractions to decimals allows for more convenient plotting of data points on graphs and charts.
Why Convert Fractions to Decimals: Why Converting Fractions To Decimals Is Essential.
Converting fractions to decimals is essential in various practical situations, mainly when working with real-world measurements, calculations, and applications.
Financial Transactions:
- Example: Imagine calculating interest on a loan or investment. Interest rates are often quoted in decimal form. Converting a fractional interest rate (e.g., 3/100) to a decimal (0.03) is necessary for accurate interest calculations.
Construction and Carpentry:
- Example: In construction, measurements for materials or dimensions are commonly expressed in decimals.
Metric System Conversion:
- Example: Converting between the metric and imperial systems often involves decimal representations. For instance, converting a fraction of an inch to millimetres requires expressing the fraction as a decimal for accurate conversion.
Percentage Calculations:
- Example: Calculating percentages involves dividing a part by a whole. Converting fractions to decimals simplifies this process, as percentages are often expressed as decimals (e.g., 25% as 0.25).
Stock and Investment Analysis:
- Example: Stock prices and financial indicators are often quoted as decimals. Converting a fractional change in stock value to a decimal is crucial for accurate financial analysis and decision-making.
Check out free Maths resources and worksheets to brush up your calculation skills.
Step-by-Step Guide: Converting Fractions to Decimals:
Numerator:
The numerator is the top number in a fraction. It represents the number of parts you have out of the whole. For example, in the fraction 3443, 3 is the numerator. It indicates that you have 3 parts of the whole.
Denominator:
The bottom number in a fraction is the denominator. It represents the total number of equal parts into which the whole is divided. In the fraction 3443, 4 is the denominator. It signifies that the whole is divided into 4 equal parts.
Decimal:
A decimal is a way of expressing numbers that are not whole. It includes a decimal point, separating the entire number from the fractional part. For example, in the decimal 2.752.75, 2 is the fundamental number part, and .75 is the decimal part.
Now, let’s go through the step-by-step guide to converting fractions to decimals:
How to Convert Fractions to Decimals
Step 1: Understand the Fraction
- Examine the given fraction. Spot the numerator (top number) and the denominator (bottom number).
Step 2: Divide the Numerator by the Denominator
- Divide the numerator by the denominator. It is the key step in converting a fraction to a decimal.
Step 3: Perform the Division
- Perform the division. You have your answer if the division results in a terminating decimal (one that ends). If it is a repeating decimal, continue the division until the pattern repeats or use the appropriate notation for repeating decimals.
Example: Convert 3/4 to a Decimal
Step 1: Understand the Fraction
- 3/4 has a numerator (3) and a denominator (4).
Step 2: Divide the Numerator by the Denominator
- =3÷4.
Step 3: Perform the Division
- 3÷4=0.753÷4=0.75. Since this is a terminating decimal, we stop here.
Method 1: Long Division: Step-by-Step Explanation
Convert ⅝ to a decimal using the long division method
Step 1: Set up the division
Step 2: Divide the Numerator by the Denominator
- Place the decimal point in the quotient above the division bracket. Begin dividing as you would in a regular long division, treating the numerator as the dividend and the denominator as the divisor.
Step 3: Continue the Division
- Bring down a zero, and continue dividing. Repeat until the division either terminates or shows a repeating pattern.
Step 4: Interpret the Result
- The result of ⅝ is 0.625
Method 2: Decimal Division
Convert ⅝ to a decimal using the decimal division method
Step 1: Set up the division
Step 2: Move the Decimal
- Move the decimal point in the numerator to the right until it becomes a whole number. Simultaneously, move the decimal point in the quotient the same number of places to the right.
Step 3: Divide
- Perform the division. Divide 50 by 8.
Step 4: Continue the Division
- Bring down a zero and continue the division until you reach the desired level of precision.
Step 5: Interpret the Result
- The result of ⅝ is 0.625.
Common Challenges and Pitfalls:
Converting fractions to decimals is a fundamental skill, but it has some common challenges and pitfalls. Understanding these challenges can help you avoid mistakes during the conversion process. Here are some common pitfalls and ways to avoid them:
Forgetting to Divide:
- Challenge: Some students may forget to perform the division when converting fractions to decimals.
- Avoidance: Remember that converting a fraction to a decimal involves dividing the numerator by the denominator.
Misplacement of Decimal Point:
- Challenge: Misplacing the decimal point from the can lead to incorrect results.
- Avoidance: Pay close attention to the placement of the decimal point.
Ignoring Repeating Decimals:
- Challenge: Repeating decimals can occur when the division does not terminate. Ignoring this and stopping prematurely can lead to inaccurate results.
- Avoidance: Be aware of repeating decimals. If you notice a repeating pattern in the division, use the appropriate notation to indicate a repeating decimal.
Overlooking Negative Exponents:
- Challenge: In scientific notation or small fractions, overlooking negative exponents can lead to errors.
- Avoidance: Understand that converting a fraction to a decimal may involve negative exponents, especially when expressing minimal values.
Applications in Real Life
Converting fractions to decimals is a practical skill with applications in various everyday situations. Here are some examples:
Shopping:
- Scenario: You’re at the store, and an item costs $1.75 per pound. You want to buy 3/4 of a pound. Converting 3/4 to a decimal (0.75) helps you calculate the cost of the amount you wish to.
Home Improvement:
- Scenario: You’re cutting a piece of wood that needs to be 2/3 of a meter long. Converting 2/3 to a decimal (approximately 0.67) helps you make precise measurements.
Financial Planning:
- Scenario: You’re planning a budget, and your monthly savings goal is 1/4 of your income. Converting 1/4 to a decimal (0.25) allows you to calculate the exact amount to save.
Interest Calculations:
- Scenario: You have a savings account with an annual interest rate of 3/100. Converting 3/100 to a decimal (0.03) allows you to accurately calculate monthly or daily interest.
Fitness Goals:
- Scenario: Your fitness plan requires you to walk 4774 miles each day. Converting 4774 to a decimal (approximately 0.57) helps you track your progress more precisely.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- It is important to Convert Fractions to Decimals for various reasons.
- The Methods for Conversion include Long Division and Decimal Division
- Common Challenges and Pitfalls include forgetting to divide in the conversion process, misplacing the decimal point or not simplifying the fraction before conversion.
- Regular practice with different types of fractions helps in mastering the process.
Quiz
Question comes here
Frequently Asked Questions
Converting fractions to decimals is essential for several reasons, spanning theoretical mathematical concepts and practical applications in everyday life.
- Decimal numbers are often more compatible with arithmetic operations (addition, subtraction, multiplication, and division) than fractions.
- Decimals provide an easier way to compare and order numbers. When dealing with fractions, it can be challenging to determine which is larger or smaller quickly. Converting fractions to decimals simplifies these comparisons.
There are the long division method and the decimal division method.
Converting fractions to decimals is a uncomplicated process, but like any mathematical operation, it’s essential to be mindful of potential pitfalls. Here are some tips to help you avoid common mistakes:
- Before starting the conversion, make sure you understand the process. Know that converting a fraction to a decimal involves dividing the numerator by the denominator.
- Whether using long or decimal division, double-check your division to ensure accuracy.
- Pay close attention to the placement of the decimal point.
- Be aware of repeating decimals. If the division doesn’t terminate and you notice a pattern repeating, use the appropriate notation to indicate a repeating decimal.
- Practice converting different types of fractions to decimals. It helps reinforce the process and familiarizes you with common patterns.
- What are some decimal conversion strategies for fractions with recurring decimals?
Example: Change the decimal 0.3333… to fraction.
Step 1: Identify the repeating digits
Here, the repeating digit is 3.
Step 2: Equate the decimal number to a variable like x.
x= 0.3333 —- 1
Step 3: Multiply both the sides by a power of ten
x=0.3333…
10 x = 10 x 0.3333
The number will become
10x = 3.3333 —– 2
Step 4: After multiplying 0.3333… with 10, the decimal point will shift
10x- x= 3.3333 – 0.3333
9x=3
Step 5: Simplify
x = 3/9 = 1/3