Exploring the Fascinating World of Triangles
Comprehensive Definition, Description, Examples & Rules
Triangles are the architects of the geometric world, subtly shaping the landscapes of mathematics and reality. With their three sides and three angles, triangles are the elementary building blocks of shapes. Let us find out how they can help you in geometry with the help of this blog created by Edulyte’s Maths experts.
Introduction to Triangles: Definition and Characteristics
A triangle is a geometric shape defined by three sides and three angles. The sum of interior angles in a triangle is always 180 degrees. Triangles are classified on the length of their sides and the size of their angles.
A triangle is crucial in geometry and trigonometry as the building block for various geometric constructions and relationships.
Understanding Triangle Shapes
Understanding triangular shapes can be confusing if you do not know their basics. Uncover each triangle type with its characteristics.
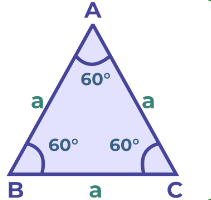
Equilateral Triangle:
- Definition: An equilateral triangle has all three sides of equal length.
- Characteristics: All three angles are equal, each measuring 60 degrees. It has a high degree of symmetry.
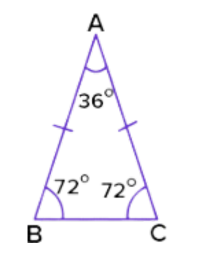
Isosceles Triangle:
- Definition: It has at least two sides of equal length.
- Characteristics: The angles opposite the equal sides are also equal.
The angle opposite the unequal side is called the base angle.An isosceles triangle’s base angles are also equal.
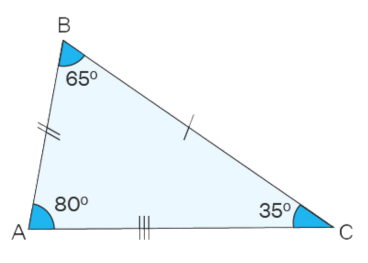
Scalene Triangle:
- Definition: A scalene triangle is one in which all three sides have different lengths.
- Characteristics: Each angle in a scalene triangle has a different measure. It lacks the symmetry present in equilateral and isosceles triangles.
Searching for the ideal Maths assistance catering exclusively to your study needs? Sign up for free and check out our tutors and find out how they can enable you to score better!
Properties of Triangles: Discover their angles and unique properties
Let us grasp the properties of triangular shapes, which will help you ace geometry. Understanding these properties of a triangle is crucial in solving geometric problems involving triangles and lays the foundation for more advanced concepts in trigonometry and geometry.
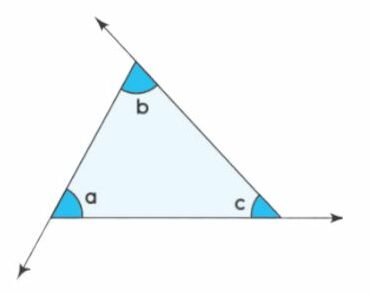
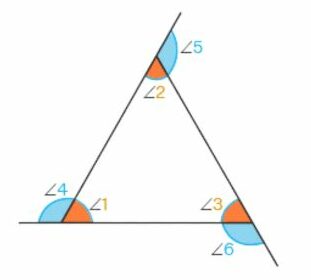
Interior and Exterior Angles
Interior Angles:
- These are the angles in a triangle.
- The three interior angles in any triangle sum up to 180 degrees.
Exterior Angles:
- An exterior angle in a triangle is formed by extending one side. The exterior angle is supplementary to the adjacent interior angle.
- The sum of the two non-adjacent internal angle measures equals the exterior angle.
Angle Sum Property:
- All interior angles of a triangle add up to 180 degrees.
Isosceles Triangle Properties:
- The angles opposite of the equal sides are also equal. This property is a consequence of the base angles theorem.
Equilateral Triangle Properties:
- All three angles in a triangle are equal in an equilateral triangle, each measuring 60 degrees. Additionally, all three sides are of equal length.
Scalene Triangle Properties:
- In a scalene triangle, none of the sides or angles are equal. Each angle has a different measure.
Triangle Inequality Theorem:
- The sum of the lengths of two sides of a triangle must be greater than the length of the third side.
Check out free Maths resources and worksheets to brush up your calculation skills.
Exploring Triangular Shapes: Beyond Traditional Triangles
Architecture:
- Architecture frequently employs triangular shapes for their structural stability and aesthetic appeal.
- Pyramids, both ancient and modern, are iconic examples. The triangular truss systems are also commonly used in roofs and bridges for strength.
Engineering and Construction:
- Triangular shapes are used to design various structures in engineering, including support systems for buildings, bridges, and towers.
- The triangular configuration distributes forces efficiently, providing stability.
Art and Design:
- Artists and designers leverage triangular shapes for visual impact and balance in compositions.
- Using triangles in patterns and designs can create dynamic and visually exciting effects.
Packaging:
- Triangular packaging is often employed for its efficiency in space utilisation and stability.
- Triangular prisms, for instance, can minimise wasted space while providing structural strength to packaging materials.
Mathematics and Geometry:
- Triangles are foundational in geometry and trigonometry, serving as the basis for various mathematical concepts.
- They are essential in calculating angles, distances, and relationships between different points in space.
Technology:
- Triangular shapes are incorporated in the design of electronic circuit boards and components, ensuring optimal distribution of components and efficient use of space.
Navigation and Surveying:
- In navigation, triangulation is a method of determining location by measuring angles from known points.
- This principle is widely used in GPS technology and surveying.
Defining Triangle Shapes
Definition of a Triangle
A triangle definition defines it as a closed geometric figure with three sides, three vertices, and three angles. It is one of the basic geometric shapes, characterised by its simplicity yet essential role in various mathematical and real-world applications.
Characteristics of a Triangle
Three Sides and Three Angles:
- A triangle is uniquely defined by having exactly three sides and three angles of a triangle.
- The combination of these elements creates a closed, three-sided figure.
Vertices:
- Triangles have three vertices, which are the points where the sides meet.
- Each vertex is associated with an angle formed by the adjacent sides.
Interior Angles:
- All interior angles of a triangle add up to 180 degrees.
- This fundamental property is valid for all triangles, regardless of their specific type.
Exterior Angles:
- Every triangle shape has three exterior angles, one at each vertex.
- The external angle at any vertex is supplementary to the interior angle at that vertex, meaning their sum is 180 degrees.
Classification by Sides and Angles
- Triangles can be categorised based on the measures of their angles as well as the lengths of their sides.
- Common classifications include equilateral (all sides and angles are equal), isosceles (two sides and angles are equal), and scalene (all sides and angles are different).
Why a Triangle is a Polygon?
Any closed two-dimensional shape having straight sides is a polygon. Triangles meet this definition as three straight sides enclose them. Therefore, a triangle is considered a polygon.
Key Attributes Setting Triangles Apart
Minimal Sides:
- Triangles have the fewest sides among polygons, making them the most straightforward polygonal shape.
Angular Sum Property:
- The interior angles of a triangle sum up to 180 degrees, a characteristic that distinguishes it from polygons with different numbers of sides.
Versatility:
- Triangles are versatile building blocks in geometry.
- They serve as the foundation for trigonometry, provide the basis for more complex polygons, and are fundamental to geometric constructions.
Stability:
- The triangular shape is inherently stable, making it a preferred choice in various applications, from architecture and engineering to packaging design.
Applications of Triangles: Their Practical Uses And Significance
Understanding triangle properties is a fundamental aspect of geometry and has broad applications in various fields. Here are several ways in which knowledge of triangle properties can be advantageous:
Geometry and Trigonometry:
- Triangles are foundational in geometry, forming the basis for more complex shapes.
- In trigonometry, studying triangles is crucial for understanding relationships between angles and sides, leading to the development of sine, cosine, and tangent functions.
Architectural and Engineering Design:
- Architects and engineers use triangular shapes in structures like trusses and girders because of their stability.
- Understanding triangle properties helps in designing load-bearing structures efficiently.
Surveying and Navigation:
- The principles of triangulation are essential in surveying and navigation.
- Surveyors use triangles to measure distances and map areas, while navigation systems like GPS rely on triangulation to determine location.
Construction and Carpentry:
- Carpenters and builders frequently use triangles for accurate measurements and to ensure the stability of structures.
- Knowledge of properties like the Pythagorean Theorem is crucial in construction.
Computer Graphics and Modeling:
- In computer graphics, understanding triangle properties is vital for creating realistic 3D models.
- Triangles are often used to represent surfaces, and algorithms based on triangle properties help render real images.
Physics and Engineering Mechanics:
- Triangular shapes are employed in physics and engineering for their structural stability.
- Concepts like resolving forces into components are based on understanding vectors, which can be represented using triangles.
Art and Design:
- Artists and designers use triangles to create visually appealing compositions.
- Understanding how triangles interact helps in achieving balance and harmony in visual arts.
Mechanical Design and Robotics:
- Engineers designing mechanical systems and robots utilise triangle properties to construct efficient linkages and ensure smooth movements.
- Triangles play a crucial role in the design of various mechanisms.
Mathematical Problem Solving:
- Many mathematical problems involve triangles, and understanding their properties enables efficient problem-solving.
- Concepts like congruence and similarity are essential in mathematical reasoning.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Triangles serve as the fundamental building blocks in geometry.
- Triangles can be classified on both sides and angles, leading to various types such as equilateral, isosceles, scalene, acute, right, and obtuse triangles.
- Understanding properties like the Pythagorean Theorem, angle sum property, and congruence criteria is essential.
- Triangles have extensive real-world applications. They provide structure stability, are crucial in navigation and surveying, and are essential in engineering, architecture, and computer graphics.
Quiz
Question comes here
Frequently Asked Questions
Equilateral Triangle:
- All three sides are of equal length.
- All three angles are equal, each measuring 60 degrees.
- The altitude, median, and angle bisectors are also equal.
Isosceles Triangle:
- Has two sides of equal length.
- The angles opposite of the equal sides are equal.
- The base angles (angles formed by the unequal side) are equal.
Scalene Triangle:
- All three sides are of different lengths.
- All three angles have different measures.
- No sides or angles are equal.
Acute Triangle:
- All angles are less than 90 degrees.
- The sum of the interior angles of a triangle is 180 degrees.
- It can be any type – equilateral, isosceles, or scalene.
Right Triangle:
- One angle is exactly 90 degrees.
- Follows the Pythagorean Theorem: a² + b² = c². In this, ‘c’ is the hypotenuse, and ‘a’ and ‘b’ are the legs.
- The sides are typically labelled as hypotenuse, opposite, and adjacent.
Obtuse Triangle:
- One angle is greater than 90 degrees.
- The sum of the angles is 180 degrees.
- It can be any type – equilateral, isosceles, or scalene.
Triangles can be classified based on both their sides and angles. Here are the classifications for triangles in each category:
Based on Sides:
Equilateral Triangle, Isosceles Triangle and Scalene Triangle
Based on Angles:
Acute Triangle, Right Triangle, Obtuse Triangle
An equilateral triangle is characterised by three sides of equal length and three angles of equal measure. In other words, it is a triangle in which all three sides and angles are congruent.
An isosceles triangle is a type of triangle that has two sides of equal length. In an isosceles triangle, the angles opposite these equal sides are also equal. The third side, called the base, is of a different length.
The Pythagorean Theorem in geometry is related to a right-angled triangle. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the lengths of the other two sides. The theorem is often expressed as: a² + b² = c²
Here:
- ‘c is the length of the hypotenuse.
‘a and ‘b are the lengths of the other two sides.