Unlocking the Mysteries of Pi : From Its Definition to Calculations and Formulas.
Comprehensive Definition, Description, Examples & Rules
Pi (π)… the enigmatic concept of mathematics whose use may have left you perplexed and dazed! Edulyte offers you insights regarding what is pi, which will empower your handling of problems related to it during tests and in other walks of life.
Introduction: Why Is Pi Important?
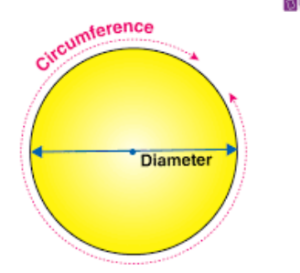
So, what is pi? Pi (π) is a mathematical constant. It signifies the ratio of a circle’s circumference to its diameter in Euclidean space. The value of pi is approximately 3.14159, but it continues indefinitely.
Importance in Mathematics:
Geometry: Pi is fundamental in geometry, particularly in measuring circles.
Circumference of a circle: C = 2πr, and the area is A = _______ where “r” is the radius.
Trigonometry: You can find pi in trigonometric functions, such as sine and cosine. For example, the sine and cosine functions have a periodicity of 2π, meaning their values repeat every 2π radians.
Calculus: Pi appears in various mathematical formulas and series and often arises in mathematical analysis and calculus.
Importance in Science:
- Physics: Pi is frequently encountered in physics, especially in problems related to circular motion, wave theory, and other phenomena involving circles and spheres.
- Engineering: In engineering disciplines, pi is crucial for calculating circles and curves.
- Computing: It is used in algorithms and computations and has a role in studying randomness and chaotic systems.
What is Pi: Definition and Significance
Pi (π) is a mathematical constant. It represents the ratio of a circle’s circumference to its diameter. The digits of pi make it an irrational number, meaning its decimal representation is non-repeating and non-terminating.
- The symbol “π” was first used by the Welsh mathematician William Jones in 1706. Leonhard Euler, the Swiss mathematician in the 18th century, later popularised the symbol of pi.
- Ancient Babylonians, Egyptians, and Greeks had approximations for the value of pi.
Significance in Geometry:
- Circumference and Area of Circles: The most fundamental application of pi in geometry is in the formulas for the circumference and area of a circle. The circumference (C) is given by C = 2πr, and the area (A) is provided by A = πr². Here, “r” is the radius.
- Volume of Cylinders and Cones: Pi is also involved in the volume formulas for cylinders and cones. The volume of a cylinder is calculated as V = πr²h, and the volume of a cone is V = (1/3)πr²h. Here “r” is the radius, and “h” denotes the height.
Significance in Trigonometry:
- Unit Circle: A circle with a radius of 1 is centred at the origin of a coordinate plane. The radian measure of angles on the unit circle is directly related to pi.
- Trigonometric Functions Periodicity: The periodicity of trigonometric functions such as sine and cosine is related to pi.
- Radians: The use of radians in measuring angles is closely tied to pi. One radian is the angle subtended when the arc length equals the radius and corresponds to an angle of approximately 57.3 degrees. The conversion factor between degrees and radians involves pi.
Check out free Maths resources and worksheets to brush up your calculation skills.
The Value of Pi : Explanation and Comparison
If you still aren’t satisfied with the explanation for what is pi, hold on. There is more. The full number of pi or value of pi (π) is commonly approximated as 3.14159. The digits of pi are an infinite, non-repeating sequence of digits.
Comparison with Other Mathematical Constants:
- Euler’s Number (e): Euler’s number, denoted as “e,” is another critical mathematical constant. It is approximately 2.71828. Both pi and Euler’s numbers appear in various mathematical formulas and are related through complex analysis.
- Square Root of 2 (√2): Square root of 2 is an irrational number, approximately 1.41421. It is another example of a mathematical constant commonly encountered in geometry and algebra.
Digits of Pi
The Pi symbol is the mathematical constant. It denotes the ratio of a circle’s circumference to its diameter, which has captivated mathematicians and scientists for centuries.
Unlike rational numbers, which can be expressed as a finite fraction, Pi’s digits never settle into a repeating pattern.
Journey Through Pi’s History:
Pursuing Pi’s precise value has been a remarkable journey throughout history. Archimedes, a Greek mathematician, developed ingenious techniques using polygons to calculate Pi with noteworthy accuracy.
The infinite series, developed by mathematicians like Isaac Newton and Gottfried Leibniz, allowed for more precise approximations of Pi.
In the 19th century, mathematicians proved that the Pi value or the pi full number is irrational, meaning it cannot be expressed as a simple fraction. While the sequence appears random, statistical tests suggest that the frequency of each digit is evenly distributed.
Pi’s Ubiquity in Mathematics and Science:
Pi’s significance extends far beyond its geometric definition. It permeates various branches of mathematics, appearing in formulas for areas, volumes, and trigonometric functions. Pi value is crucial in physics’s motion, gravitation, and electromagnetism formulas.
Pi’s ubiquity in mathematics and science underscores its fundamental nature. It serves as a bridge between different fields, connecting geometry, trigonometry, and physics.
Searching for the ideal Maths assistance catering exclusively to your study needs? Sign up for free. Check out our tutors and get classes customised to your specific learning needs!
Pi Symbol: Origin and Significance
The pi symbol π can be traced back to the 17th century when Welsh mathematician William Jones introduced it in his work “Synopsis Palmariorum Matheseos.”
The adoption of π as the symbol for pi was not immediate. Still, it gained widespread acceptance over the following decades, mainly due to the influence of Swiss mathematician Leonhard Euler.
Cultural and Mathematical Significance
It has become a cultural icon, symbolizing precision, complexity, and the pursuit of knowledge. Its infinite and non-repeating decimal representation has sparked curiosity and inspired countless art, literature, and music works.
Pi’s significance is also evident in its numerous applications in science and engineering. From calculating the circumference of the Earth to designing efficient algorithms, pi plays a crucial role in various fields. Its presence in these real-world applications highlights its practical importance.
How to Calculate Pi : Different Methods And Approaches
There are traditional approaches and modern algorithms to calculate the value of pi.
Traditional Methods
- Geometric Methods: Early civilizations employed geometric methods to approximate Pi’s value. One common approach involved inscribing and circumscribing regular polygons within a circle and calculating their perimeters.
- Archimedes’ Method: Archimedes, a Greek mathematician, divided the hexagons into triangles and calculated their areas, demonstrating that the ratio of the inscribed hexagon’s area to the circle’s area is approximately 0.7854.
- Infinite Series: Mathematicians like Isaac Newton and Gottfried Leibniz discovered infinite series that, when summed, converge to calculate the value of Pi value with remarkable accuracy.
Modern Algorithms
- Bailey-Borwein-Plouffe (BBP) Formula: In 1995, David Bailey, Peter Borwein, and Simon Plouffe developed a groundbreaking algorithm that generates digits of Pi directly without requiring intermediate calculations.
- Chudnovsky Formula: The Chudnovsky brothers’ formula, George and David, utilises the properties of special functions to generate Pi digits with exceptional speed.
- Monte Carlo Method: The Monte Carlo method, a computational technique based on random sampling, can also be applied to Pi calculation. By randomly generating points within a square and counting those that fall within an inscribed circle, one can estimate Pi’s value with increasing accuracy as the number of samples increases.
Pi Number in Full And Irrational Numbers
Pi cannot be represented entirely using a finite number of digits. It is an irrational number. It means the decimal representation never ends and never repeats. The pi full number cannot be written; its value for calculations is taken as 3.14159
Concept of irrational numbers
An irrational number is a number that cannot be expressed as a finite fraction of two integers. It means that their decimal representations never end and never repeat. Irrational numbers are abundant in mathematics and are essential for many mathematical concepts, including geometry, trigonometry, and calculus.
Pi Formulas: Overview And Applications
Pi (π) is used in various mathematics, physics, and engineering formulas. The pi formulas enable students, engineers and even people from other fields to calculate quickly.
Formulas involving Pi in Geometry
- Circumference of a circle:
C = 2πr, C is the circumference, r is the radius.
- Area of a circle:
A = πr²
where A is the area, r is the radius.
- Volume of a sphere:
V = (4/3)πr³ ; V = volume, r = radius.
- Surface area of a sphere:
S = 4πr²
where S is the surface area, r is the radius.
Formulas involving Pi in Trigonometry
- Definition of sine (sin):
sin(θ) = y/r
where θ is the angle, y is the opposite side, and r is the hypotenuse.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Pi is an irrational number. It means that its decimal representation never ends and never repeats.
- Ratio of a circle’s circumference to its diameter is represented by pi (π).
- Pi has been calculated to trillions of digits, but its decimal representation continues infinitely.
- Pi is used in various formulas in mathematics, physics, and engineering.
- Pi is a symbol of mathematical beauty, precision, and the infinite nature of mathematics.
Quiz
Question comes here
Frequently Asked Questions
The Pi symbol, represented by the Greek letter π, denotes the mathematical constant pi. Pi is approximately equal to 3.14159, but its decimal representation never ends and never repeats. The symbol π was first used in this context by Welsh mathematician William Jones in his 1706 work “Synopsis Palmariorum Matheseos.”
It is an irrational number. It signifies that its decimal representation never ends and never repeats. However, we can calculate pi to any desired degree of accuracy.
Pi is an irrational number. It signifies that its decimal representation never ends and never repeats. It cannot be expressed as a finite fraction of two integers.
Pi (π) is an irrational number. It signifies that its decimal representation never ends or repeats. As a result, pi has an infinite number of digits.