
Unlocking the World of Area Formulas: Mastering Math's Geometric Gems
Comprehensive Definition, Description, Examples & Rules
Introduction to Area Formulas
Area formulas help us find out the amount of space occupied by various kinds of shapes. In real life, calculating the area of different kinds of spaces helps us correctly determine the stretch of a particular space enclosed by a boundary. This procedure is beneficial in the profession of architecture and construction to decide reasonable and accurate prices of land.
Common Area Formulas
Here is a list of various kinds of commonly found geometric shapes and their respective formulas:
Squares
A= s^2
Where
‘A’: is the area of the rectangle.
‘s’: is the measure of any one side of the square as all sides are equal.
Rectangles
A= l * b,
‘A’: area of the rectangle.
‘l’: length of one of the sides of the rectangle.
‘b’ refers to the breadth of one of the sides of the rectangle.
Triangles
A= ½ * b * h
Where
A is the area of the triangle
b is the base of the triangle
h is the height of the triangle
Circles
The area of circles is computed with the help of the formula:
A= πr^2
Where ‘r’ is used to denote the radius of the circle.
Area of Rectangles and Squares
Here is a representation of the area formulas for squares and rectangles
Squares
A= s^2,
‘A’: the area of the rectangle.
‘s’: the measure of any one side of the square as all sides are equal.
Example:
What would be the area of a square with a side of 10 cm?
Answer:
A= 10^2
A=100 cm^2
Rectangles
A= l * b,
‘A’: area of the rectangle.
‘l’: length of one of the sides of the rectangle.
‘b’ refers to the breadth of one of the sides of the rectangle.
Example:
Find the area of a rectangle with length= 10 cm and breadth= 4 cm.
Solution:
A= 10*4
A= 40 cm^2
Area of Triangles
Here is a representation of the different formulas used to compute the area of different triangles:
Isosceles Triangle
A=½ * b* h
(where ‘A’ refers to the area of the triangle, ‘b’ refers to the base, and ‘h’ refers to the height of the triangle).
Example: Find the area of an isosceles triangle with a base equal to 50 cm in length and height equal to 10 cm.
Solution: Given that the base of the triangle is up to 50 cm in length and height is equal to 10 cm, using the formula for area for isosceles triangles, we get:
A= ½*
A= ½*50*10
A=½*500
A= 250 cm^2
Scalene Triangle
A=½ * b* h
(where ‘A’: is the triangle’s area, ‘b’: is the triangle’s base, and ‘h’: is the triangle’s area).
Example: Find the area of a scalene triangle with a base equal to 30 cm in length and height equal to 4 cm.
Solution:
A= ½*
A= ½*30*4
A=½*120
A= 60 cm^2
Equilateral Triangle
A= √3/4 * s^2
(where ‘A’: is the area of the triangle and ‘s’: is the length of the equal sides of the triangle)
Example: Find the area of an equilateral triangle with a side equal to 8 cm.
Solution:
A= √3/4 * 8^2
A=√3/4 * 64
A=√3*16
A=1.732*16
A= 27.712 cm^2
Area of Circles
The formula for calculating the area of circles is given as A= πr^2
Where ‘r’ is used to denote the radius of the circle.
Area of Sectors
A portion of a circle that is covered by two radii (plural of radius) and the corresponding arc is known as the sector of the circle.
The area of a sector is computed with the help of the formula:
A= θ/360 * πr^2
Where θ corresponds to the angle that is formed by the two radii.
Area of Segments
A portion of a circle that is covered by a chord and the corresponding arc is known as the segment of the circle.
The area of a sector is computed with the help of the formula:
A= 1/2r^2 (θ – sin θ)
Where θ corresponds to the angle that is formed by the chord.
Area of Trapezoids
The area of a trapezoid can be computed using the given formula:
A= b1 + b2 / 2 * h
‘A’: is the area of the rectangle.
‘b1’ and ‘b2’ refer to the length of the bases or the two equal sides.
For cases when all the required measurements are not provided, you can use the transposing method to find out the required measurements.
Example
Find the area of a trapezoid with b1 as 6 cm, b2 as 4 cm, and height as 2 cm.
Solution
Given the following measurements, using the formula to find area of a trapezoid, we get,
A= 6+4/2*2
A=10/2*2
A=5*2
A=10 cm^2
Area of Parallelograms
A parallelogram’s area can be determined using the formula:
A= b * h
‘A’: the area of the rectangle.
‘h’ is the parallelogram’s height.
‘b’ refers to the measure of the base of the parallelogram.
The area formula for parallelograms is closely related to that of rectangles and squares. Rectangles can be seen as special cases of parallelograms where the opposite sides are equal in length and all the angles are 90 degrees each. Similarly, squares can be seen as special cases of rectangles and parallelograms where all the sides are equal in length and all the angles are 90 degrees each.
Area of Rhombuses
The area of rhombuses can be calculated with the help of the formula:
A= d1*d2/2
(d1 and d2 are the specific measurements of the two diagonals)
The diagonals of a rhombus are line segments that connect the opposite vertices. A unique property of rhombuses is that these two diagonals are perpendicular bisectors of each other. This unique property plays a crucial role in producing the area formula for rhombuses.
Area of Regular Polygons
Areas of regular polygons like pentagons, hexagons and octagons can be computed using the formula:
A= 1/4n*s^2 ÷ tan (π/n)
n: number of sides in a polygon
s: length of side
Substituting the number of sides for respective polygons in the place of n can give us the final result. For example, since a pentagon has 5 sides, its area formula will have 5 in place of ‘n’, a hexagon will have 6 and an octagon will have 8.
Example: Find the area of an octagon with a side equal to 10 cm.
Solution: given the side equal to 10 cm and the number of sides equal to 8, we get:
A= ¼*8*10^2 ÷ tan (π/8)
A=2*100÷ 2-1
A= 200÷ 0.4142
A= 482.85 cm^2
Advanced Area Formulas
The following given methods are employed when attempting to calculate the area of lesser-known shapes:
- Irregular shapes: The irregular shape should be sectioned into various shapes that are more commonly known. Following this, compute the areas of all the shapes you are familiar with and sum them all up to figure out the approximate area of the irregular shape.
For example: Any shape that is not so common can be further sectioned into more commonly known shapes like squares, rectangles, triangles, etc. to know the total area estimate.
- Sectors of Circles: you can know the area covered by a sector of a circle by using the given formula equation:
A= 1/2r^2θ
(θ: included angle between the two radii).
Example: For a circle with a radius of 4 cm and the included angle between the radii as 90 degrees, the area of a sector can be computed as:
A= ½*4^2*π/2 (θ=π/2 )
A=8*3.14/2
A=12.56 cm^2
Real-World Applications
All area formulas have various uses in a variety of real-world applications, like:
- In architecture, interior spaces can be designed using area formulas.
- In engineering, dams can be designed and traffic can be managed efficiently using area formulas.
- In physics, area formulas can be used in thermodynamics, fluid dynamics, and other fields.
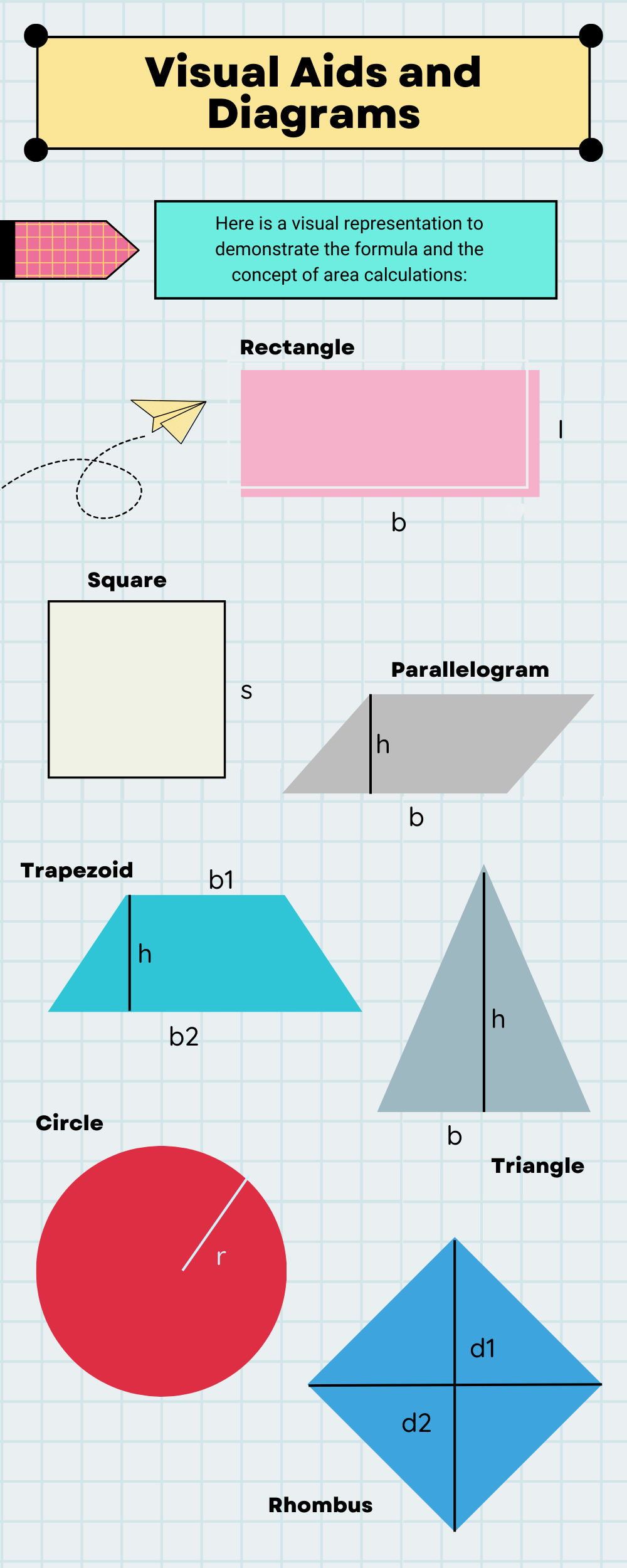
Infographics: Visual Aids and Diagrams
Here is a visual representation to demonstrate the formula and the concept of area calculations:
Tips and Tricks
Here are some tips and shortcuts to calculate the math area formulas quickly and accurately:
- Divide complex shapes into familiar ones.
- Remember the commonly used formulas like those of squares, rectangles, triangles, etc.
- If the shape is symmetrical, try dividing it into two equal shapes and multiply the result with the number of symmetrical parts to compute areas quickly.
Common Mistakes to Avoid
Have a look at the following common errors committed while computing areas of different shapes and their preventive measures:
- Avoid using the wrong area formulas for the wrong shapes. Remember the specific area formulas for each kind of geometrical shape to avoid discrepancies.
- Avoid using different units while calculating and maintain the same units throughout the formula.
- Avoid missing crucial steps in certain area formulas like dividing the product of base and height by 2 in triangles, squaring the radius in circles, etc.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Area calculations help us find out the amount of space occupied by various kinds of shapes.
- Area calculations are used in various real-life applications like engineering, physics, architecture, etc.
- Remember the specific area formulas for different shapes for accurate calculations.
Quiz
Question comes here
Frequently Asked Questions
For isosceles(used when two sides are equal) and scalene triangles(used when all sides are unequal), the formula to find area stands as ½*b*h, whereas for equilateral triangles (used when all sides are equal), it is A= √3/4 * s^2.
The formula for calculating the area of circles is given as A= πr^2
Where ‘r’ is used to denote the radius of the circle.
The area of a trapezoid can be computed using the given formula:
A= b1 + b2 / 2 * h
It is useful in times when we need to compute the area of a shape in the form of a trapezoid.
Parallelograms are quadrilaterals that have opposite sides that are parallel to each other. The area of a parallelogram can be computed using the formula: A= b * h
The area of rhombuses can be calculated with the help of the formula:
A= d1*d2/2 (d1 and d2 are the lengths of the two diagonals)
For irregular shapes or polygons with more than four sides, you need to divide the irregular shape into commonly known shapes.



