Understanding Circumference and Perimeter of Circles
Comprehensive Definition, Description, Examples & Rules
Introduction to Circumference and Perimeter
While the circumference and perimeter share similarities, there’s a fundamental distinction between these two terms. The perimeter refers to the length of the outline of a shape with straight sides, while the circumference specifically pertains to the length of a circle’s outline. The concept of circumference relates to the complete distance around the curved geometric shape.
Importance in Geometry
The importance of circumference and perimeter in geometry is:
- It helps to identify the length of the outline and determine the surrounding length, which helps to calculate geometrical calculations.
- The circumference and perimeter will also help you quantify a physical shape and provide a foundation for advanced trigonometry, algebra, and calculus mathematics.
Importance in Real-life Application
The significance of circumference and perimeter in real-life application is:
- Calculating the circumference of your waist is something you are doing in the form of the shape of a circle, not an exact circle, but the principle calculation is similar.
- Civil engineers are the primary users of both the perimeter and the circumference formula in real life, as building and construction require this calculation to a great extent.
How to Find the Circumference of a Circle?
The circumference of a circle is the measurement of the circle’s boundary, defined as the region occupied by the outside line. If you open the circle and make it in the form of a straight line, the length of the line will be the circumference of the circle, which is measured in single units — cm, m, inch.
The Step-by-Step guide to follow is:
- First, you must use the circle’s radius to calculate the shape’s exact circumference.
- If the circle’s radius is not provided, then you have to use the circle’s diameter to calculate the radius.
- Then, use the formula and the value of Pi.
The formula is:
- C = 2πr
Here, c is denoted as the circle’s circumference, while r is the circle’s radius.
The value of pi can be used as 22/7 or 3.14159.
Or
- C = 2√πA
It is the formula you use when you do not have the radius or diameter, but the area of the circle is provided.
Visual Representation
Circumference Formula Explained
Suppose you break down the components of the circumference formula. In that case, you have to denote that you are multiplying the value of pi with the circle’s radius and then multiplying the exact value by two, which will help you calculate the circle’s circumference.
The significance of π (pi) in the formula is very high as it is a Greek letter of the mathematical term discovered as a constant equal ratio of the circumference of a circle to its diameter, so the number is calculated in decimal points. It’s of higher clarity in the circle circumference formula.
Example:
If the diameter of the circle is 20 cm, find the circumference of the circle
Solution:
The radius of the circle is exactly half of the diameter.
So,
radius = diameter/ 2
= 20/2
= 10 cm
So,
Circumference = 2πr
= 2×22/7×10
= 62.86
So, the circumference of the circle is 62.86 cm
Finding the Perimeter of a Circle
The perimeter in the context of a circle is similar to that of the circumference. Still, the perimeter is a word used for single-line shapes, especially rectangles, squares, or triangles. The circumference is commonly used for circular shapes that do not have a side. The perimeter is commonly used for shapes that consist of a side.
The formula to calculate the perimeter of the circle is similar to the circumference of the circle itself, which is:
- 2πr
The circle’s perimeter and circumference are similar because both have similar formulas and meanings. Just as the circle is a shape without any sides, it does not offer the use of the word perimeter.
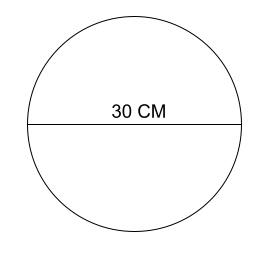
Circle Circumference Formula In Action
Real-world practical visual examples for calculating the circumference of the circle
Calculate the circumference of the circle with a diameter of 30 cm
Solution:
The radius of the circle is exactly half of the diameter.
So,
radius = diameter/ 2
= 30/2
= 15 cm
So,
Circumference = 2πr
= 2×22/7×15
= 94.29
So, the circumference of the circle is 94.29 cm
Comparing Circumstance and Area
The length of the outline of a particular shape is the perimeter or the circumference of the circle, but the area is the total amount of space consumed inside the outline shape of the circle. The perimeter is the outside region, while the area is the inside region.
The uses of the circumference and the area are different in various situations, such as when calculating the outline border of a particular region, you use the circumference formula, while when calculating the area inside a particular shape, you have to use the area of the circle formula.
Perimeter of Circle vs. Perimeter of Other Shapes
The circle’s perimeter is known as the circumference of the circle, as you use the word perimeter when the shape has a particular side. The circle is not a plane figure, and the boundary of a plane figure, such as a triangle or a square, is the perimeter, while the circle is a circumference calculation.
The formula to calculate the circumference or perimeter of the circle differs from the formula you have to use to calculate the perimeter of the other shapes. If you add all the sides of the other shapes, you will get their perimeter, but you have to use a different formula for the circle.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The Perimeter or the circumference is a similar thing.
- The perimeter is calculated for shapes like triangles, rectangles, and squares, while the circumference is calculated for circles.
- The radius of the circle is half of its diameter.
- You can also calculate the circumference of the circle by using its area and without the presence of the radius of the circle.
Quiz
Question comes here
Frequently Asked Questions
The circumference of a circle is simply the distance around its outer border. If you were to straighten out the curved line that makes up the circle, the length of that line would be referred to as the circumference. The formula that you have to use to calculate the circumference of the circle is:
- C = 2πr
There is no direct difference between the circumference and perimeter of a circle as the word circumference is used for circles while the word perimeter is used for the straight line length shapes that consist of a side. For the other shapes, you add up the sides and you calculate the perimeter, but for the circle unit, use a formula for which it is known as the circumference.
The value of PI is the ratio of the circle’s circumference to its diameter, and the value is an approximate value by which you can divide the circumference and get the exact value of your circumstance. It plays a very important role in your calculation, and to find the most of the circle’s values, you have to use the π (pi) for accurate calculation.
The circle’s circumference has a direct relationship with its area, as you can find the area of a circle by taking the product of half of the circumference and the radius of the circle. There is also a formula that you can use to calculate the circumference of the circle using the area when the radius is not provided in the formula:
- C = 2√πA
Yes, It is possible to find the circumference of a circle without knowing its radius. If the area of the circle is provided, then you can use that formula to calculate its circumference as:
- C = 2√πA