Navigating the Mathematical Frontier: The Secrets of Asymptotes Unveiled
Comprehensive Definition, Description, Examples & Rules
Exploring Asymptotes
An Asymptote is a straight line that directly approaches a particular curve but does not meet that curve at any infinite point or distance. Asymptotes are the line that the curve will approach and move towards infinity. It is an essential part of mathematics and has an important step in sketching graph equations.
Significance
The significance of Asymptotes are:
- It conveys information about the particular behavior of a curve in a large number.
- It helps solve graphical solutions easily, and sketching the graph also becomes very easy using an Asymptote.
- The study of Asymptotes broadly is known as asymptotic analysis.
- It will also help you to determine how the function will behave at the edge of a particular curve.
- It consists of three types: vertical, oblique, and horizontal, which have different meanings and functions separately.
Asymptotes: A Detailed Definition
What is Asymptote?
In analytical geometry, asymptotes definition is a curve or a line approaching zero as one or both coordinates are infinity. The line is the tangent to the curve at a point of infinity. You can define it as a straight line that constantly approaches a particular curve but does not meet that curve at an infinite distance.
Role
The role of an Asymptotes in the study of graphs and functions includes:
- It helps to review rational functions and discover undefined values in the graph.
- An Asymptote will help you find the direction in which the graph will go and also find the X values.
- You will not be able to find the exact value, but you will reach close to the value that you want to find out.
Vertical Asymptote Vs. Horizontal Asymptote
A vertical Asymptote of a graph is a vertical line denoted by ‘x’ where you can see that the graph is towards the positive or negative infinity as the inputs are ‘a’. The vertical Asymptote occurs when the denominator of a rational function approaches zero. A horizontal Asymptote is a horizontal line denoted ‘y’ where the graph approaches the line from infinity to minus infinity.
Vertical Asymptote Characteristics and Applications
The characteristics and applications of the Vertical Asymptote are:
- It occurs to the values that make the denominator zero.
- A dotted vertical line represents it.
- It represents a value that a rational function is undefined, so the value is not the function’s domain.
Horizontal Asymptote Characteristics and Applications
The characteristics and applications of the Horizontal Asymptote are:
- The numerator is less than the denominator in degrees.
- It also occurs when the numerator degree is equal to the degree of the numerator.
- It is a horizontal line that is not part of the graphical function but has significant importance in the value of ‘x.’
Understanding Asymptote Equations
The Asymptote Equation is a basic calculation you follow for all the types of the Asymptote. All the types of different equations, and you can express them differently in the form of graphs.
Vertical Asymptote
You can derive the vertical Asymptote as:
x = a for the graph function y = f(x)
Conditions that it serves:
- lim x→a – 0 f(x) = ±∞
or
- lim x → a + 0 f(x) = ±∞
Or, one of the side limits, x = a, shall be equal to infinity.
Oblique Asymptote
You can derive the oblique Asymptote as:
y = f(x) where the straight line equation will be y = kx + b
The two limits finite are:
- limx → +∞ f(x)/ x = k
and
- lim x → +∞ [f(x) – kx] = b
Horizontal Asymptote
You can derive the horizontal Asymptote as:
y = f(x) and for straight-line functions y = b
The limit finite is:
limx → +∞ f(x) = b
Graphical Representation of Asymptotes
The graphical representation of the Asymptote is different for all three types of Asymptote. These are:
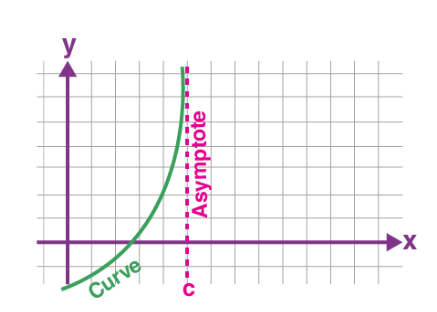
Vertical Asymptote
For the vertical Asymptote, X approaches some constant value of C from the left side to the right side, and the curve will move forward towards infinity (±∞). The representation on the graph is as follows:
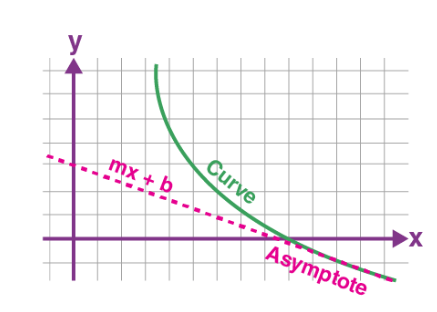
Oblique Asymptote
The oblique Asymptote is when x moves towards infinity (±∞), and the curve will move towards a line made from the y = mx + b equation. The representation of the oblique Asymptote graph is:
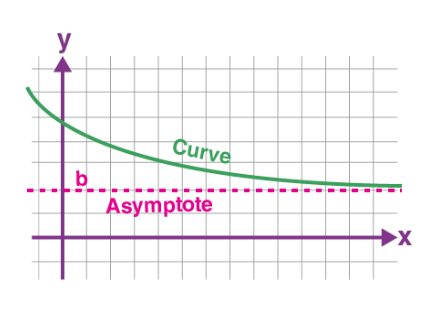
Horizontal Asymptote
The horizontal Asymptote is when X will be from minus infinity, and the curve will approach some constant value of b. The graphical representation of the horizontal Asymptote includes:
The Asymptote Formula
The equation for Asymptote can be derived by using a specific formula, and these include:
- x = a
- y = a
- y = axe + b
- lim x f(x)
- lim x – f(x)
- y = mx + b
Example:
Find the Asymptote of the equation f(x) = (3x – 2)/(x + 1)
As Vertical Asymptote:
Here, f(x) is undefined, so, x = -1
Finding the one-sided limits
limx →- a – 0 f(x) = limx→- 1 – 0 3x – 2/x + 1 = – 5/-0 = +∞
limx →- a + 0 f(x) = limx→- 1 + 0 3x – 2/x + 1 = – 5/0 = -∞
So, function f(x) has a vertical Asymptote at x = -1
As Horizontal Asymptote:
So, x → ±∞
limx →±∞ f(x) = limx→±∞ 3x – 2/ x + 1 = limx→±∞ (3 – 2/x)/ (1 + 1/x) = 3/1 = 3
So, function f(x) has a horizontal Asymptote at y = 3
Asymptotes in Rational Function
Rational functions are an essential part of mathematics. These are the functions written in polynomial functions and have an effective role of Asymptote in it. The role of Asymptote in rational function includes:
- The denominator equals zero for a particular value, and the denominator also increases in certain situations, which helps to calculate the rational functions.
- The rational functions that have a denominator of zero common causes of Asymptote.
- The domain of a Rational function includes all the real numbers except the value zero, and Asymptote helps to determine this value.
Examples:
Find the domain and all asymptotes of the function: Y= x² +3x +1
4x² – 9
Solution:
4x² – 9 = 0 (take denominator as zero)
x²= 9/4 = 3/2
Y = x²/ 4x²
= 1/4
Domain x ≠ 3/2 or -3/2, Vertical asymptote is x = 3/2, -3/2, Horizontal asymptote is y = 1/4, and Oblique asymptote = none
Asymptote Rules and Guidelines
There are rules you need to follow, which will help you calculate the Asymptote and make your calculations easy. These include:
- If n is less than m, then the Asymptote is y = 0
- If n is equal to m, then the Asymptote is y = a/b
- If n is greater than m, then the Asymptote is nil.
Practical Tips are:
- You need to identify the Asymptote that is required to be calculated in that particular sum.
- You need to understand the properties, rules, and regulations of the Asymptote.
- Using zero in these sums is essential, and you must use it appropriately.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Asymptotes play a significant role in calculus and limits and are one of the most essential mathematical calculations for rational functions.
- There is a set of rules and guidelines that are important to follow while calculating the Asymptote.
- It is an essential part of mathematics and requires a lot of patience while calculating as it involves a lot of hidden calculations.
- Zero is the most important number while calculating an Asymptote.
Quiz
Question comes here
Frequently Asked Questions
The horizontal Asymptote is a horizontal line on the graph, determined as y = b. In the graph, the line can be an input approach from plus infinity or minus infinity, slanted by the line y = mx + b. The slanted line can also approach from plus infinity to minus infinity.
The basic Asymptote equations are :
- x = a
- y = a
- y = ax + b
These are the basic equations that you divide into further equations and it helps you calculate and find out the exact value you want.
The asymptote rules and guidelines that you need to follow while calculating Asymptote are:
- If n is greater than m, then the Asymptote is nil.
- If n is equal to m, then the Asymptote is y = a/b
- If n is less than m, then the Asymptote is y = 0
Asymptote has a vital role in calculus as it simplifies approximation for complex equations, and these are useful graphic rational equations that are relevant to rational functions and calculus that helps to calculate the limits of function as well.
Yes, there are different types of Asymptote. These include:
- Vertical Asymptote
- Horizontal Asymptote
- Oblique Asymptote
The common misconceptions or errors are:
- Calculating in the long place values and making errors in addition and subtraction is very much possible in Asymptote.
- People always mess up while calculating, and they mess up the rules and guidelines.
- It is important to know the positive and negative figures, which is one of the errors people commit while calculating Asymptote.