Exploring Pyramids: Shapes, Properties, and Examples
Comprehensive Definition, Description, Examples & Rules
Introduction to Pyramids
A pyramid is considered a three-dimensional shape consisting of a polygonal base and a flat triangular face that joins through a common point called Apex. A pyramid can be formed by connecting the bases of the shape to an Apex. Each edge of the base of the pyramid is connected to its Apex and forms the triangular face that is also known as the lateral face.
Significance in Geometry
The significance of the Pyramid in geometry is:
- It consists of many geometrical properties, which are important in mathematical analysis and study.
- It has essential properties of height and base that are important for mathematical equations.
- Calculating the total surface area and the lateral surface area of the pyramid is an essential significance of the shape.
Pyramid Definition
A pyramid is a three-dimensional structure with a polygonal base, and the other flat surface of the pyramid replicates the Triangle. This is your answer for what is a pyramid. After connecting all the bases of the pyramid to its Apex, it is how you can form the shape.
The primary characteristics of a pyramid are:
- It is a three-dimensional shape.
- It consists of a polygonal base with a flat triangular face joining at the common point called Apex.
- After connecting all the edges of the base you can form a triangular face known as the lateral surface of the pyramid.
Types of Pyramids
There are various types of pyramids that are a part of geometry. These are:
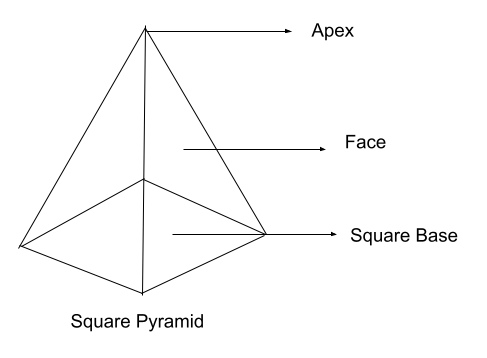
Square Pyramids
A square pyramid is a three-dimensional geometric shape that has a square base and also has four triangular faces that meet at a single point. A square pyramid is also called a Pentahedron.
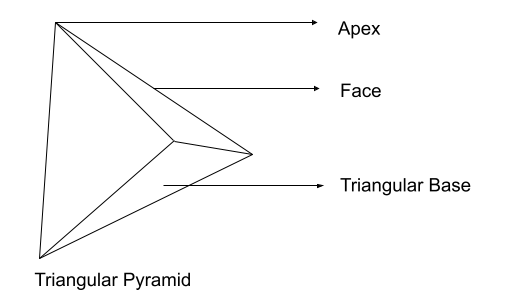
Triangular Pyramids
The most common type of pyramid is the triangular pyramid. It is a geometrical shape with three triangular faces and a triangular base. A triangular pyramid is also known as a tetrahedron composed of straight edges and vertices.
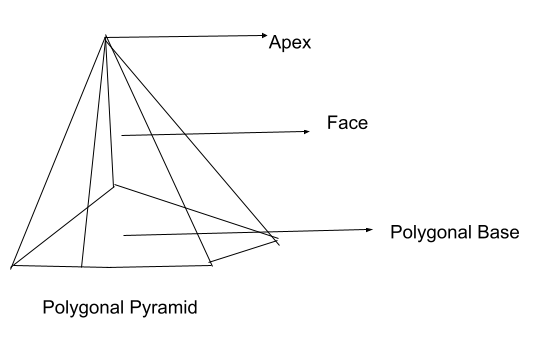
Pentagonal Pyramids
A pyramid that consists of a pentagonal base is known as a pentagonal pyramid. It has a base like a regular pentagon and consists of lateral bases equivalent to an equilateral triangle.
The differentiation in the types of pyramids happens according to the basis that these pyramids have.
3D Pyramid Visualisation
A Pyramid is a three-dimensional shape with a height, base, and side. The three-dimensional features of a pyramid are very easy to describe as it is the shape that looks different from different positions and you cannot draw it from a different perspective. The great pyramids in Egypt are a primary example for you to visualize the 3D pyramids and how they consist of three dimensions.
Prism Vs Pyramid
The primary difference between a prism and a pyramid is their shape and the number of faces that these shapes have. A prism consists of two identical parallel bases which are directly connected by a flat side while on the other hand, a pyramid has a single base and triangular side which meet at a point known as the apex. A pyramid consists of five faces, while a prism differs in the number of faces according to its shape.
Pyramid Height
The base of the pyramid is always a polygon and the face of the pyramid is always a triangle. The triangular side meets a common point known as the apex, which is the topmost point of the pyramid. The height of the pyramid will be the perpendicular distance calculated from the apex of the pyramid to the center of the base of the pyramid.
Calculating the height of the pyramid for all types of pyramid that has a polygonal base will require the usage of the Pythagoras Theorem which will help to calculate the height or slant height of the pyramid.
Edges and Vertices of A Pyramid
A regular pyramid consists of five faces, five vertices, and eight pyramid edges. All these properties of the pyramid contribute to the making of the shape which leads to a successful creation. Pyramid, indeed, is a very effective shape that has good importance for all its properties.
How to Draw a Triangular Pyramid?
The step-by-step instructions to follow the triangular pyramid are:
- To create a pyramid, draw a line from the center of the triangle going upwards. This line represents the height of your pyramid.
- To form the top point of the pyramid, known as the apex, you should connect it to each corner of the triangle.
- These connections will create the edges of the pyramid.
The base of a Pyramid
A pyramid is a solid figure because of the properties of the base of a pyramid. The base of a pyramid is always a polygonal shape and determines the structure of the entire shape. The pyramid’s base has direct connections with the triangular faces of the pyramid and helps you to determine the types of the pyramid.
Pyramid Sides
A pyramid generally consists of five faces, known as the five sides. It generally consists of triangular sides and most of the pyramids are of triangular base but it also consists of a further polygonal side, especially for a certain pyramid. The different types of pyramid define the size of the pyramid and joining the edges and the faces of the pyramid to the apex create a complete pyramid.
How to Draw a 3D Pyramid?
Drawing a regular pyramid is easy but if you want to draw a three-dimensional pyramid then it might be a bit challenging. The process includes:
- First, you have to start by drawing the left side of your pyramid.
- Then, outline the top region of your pyramid.
- Following this will be the left bottom part of the pyramid you are drawing.
- Complete the shape by directly joining all the lines.
- Then draw the dimensions of the pyramid.
- Draw certain patterns on the left side, which will ensure a 3D nature.
- This is how you can easily create an effective pyramid.
- Following these steps will help you to create a proper 3D pyramid.
Pyramid Angles
The general pyramid consists of an equilateral triangle inside it which makes its Apex aligned about the centre of the base making the internal angles of the pyramid measure 60 degrees. The angles of the pyramid differ according to its type, especially the type of base the pyramid has and if the pyramid has a hexagonal base then the angles will be 120 degrees.
Pyramid Properties
The primary properties of the pyramids are:
- Pythagorean Theorem: In the sums where the height or the slant height of the pyramid is not provided for that sum, you have to use the Pythagorean theorem to calculate the height of the pyramid and determine the further properties equivalently.
- Volume formula: The volume of the pyramid is (length × width × height)/3.
Infographic: "Pyramids Unveiled"
The example of Pyramid are:
Real-world examples of a Triangular Pyramid are Temples, Churches, and Huts.
The real-world example of a Square Pyramid is the pyramid of Giza.
The real-world example of a Polygonal Pyramid is Pyramid in Egypt.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A pyramid is a necessary shape that mostly consists of polygonal bases.
- Pyramid consists of many properties and has three three-dimensional shapes, which is essential for mathematical calculations.
- For geometry, pyramids are essential and have a high role to play in geometrical calculations.
Quiz
Question comes here
Frequently Asked Questions
To calculate the height of the pyramid, you can use the sum given to you. Use the Pythagorean theorem and determine the largest angle of the pyramid. Then, apply a triangle formula to calculate its height.
A regular pyramid comprises five vertices, five faces, and eight edges. All these properties of the pyramid contribute to the making of the shape a successful creation.
The step-by-step guide on drawing a 3D pyramid is:
- First, start with drawing the left side of your pyramid.
- Outline the top region of your pyramid.
- Draw the left bottom part of the pyramid next.
- Complete the shape by directly connecting all the lines.
- Then, draw all the dimensions of the pyramid.
- Draw particular patterns on the left side to ensure a 3D nature.
- Following these steps will help you to create a proper 3D pyramid.
The properties of a pyramid, especially the right pyramid, are:
- One of the angles of the right pyramid day is 90 degrees while other angles of the pyramid are specially equilateral triangles with 60 degrees each.
- A pyramid consists of 5 vertices and eight edges, and 5 faces or sides.
- The formula to calculate the volume of a pyramid is (length × width × height)/3.