Mastering Trigonometry: Cosine (cos) and Cosine Squared (cos²) Formulas
Comprehensive Definition, Description, Examples & Rules
Introduction
A field of mathematics that handles the relationship between sides and angles of triangles is called trigonometry. Trigonometry finds application in miscellaneous fields like engineering, physics, astronomy, and architecture. One of the most important of the various trigonometric functions is cosine or simply cos. The cosine function represents the ratio of the angle of a right triangle to and the measure of the side adjacent to the hypotenuse (which is the longest side in a right triangle, facing opposite the right angle). The cosine function is used to solve a variety of problems that we face every day like finding particular angles and measure of distances. The same function when squared is mathematically represented as cos^2 and also comes in handy in an array of real-world scenarios such as problems relating to alternating current in physics and engineering, statistics, and more.
Cosine (cos) Formula
The cosine function or cos is a function in trigonometry that shows us how the angle of a right triangle relates to the side that is adjacent to the hypotenuse or the longest side in a right triangle. Mathematically, for any given angle, say θ, the cos theta formula can be represented as:
Cos θ = measure of the side adjacent to the hypotenuse/ measure of the hypotenuse
The cosine function is an essential component of trigonometry. It is used in various tasks like finding the relationship between angles in a right triangle, discerning the various attributes of periodic occurrences, solving problems related to circular problems, etc.
The general formula for cosine (cos) about a point on the unit circle with coordinates as x and y, is given as:
Cosθ = x
Since the length of the radius in a unit circle is always 1,
x^2 + y^2 = 1
Hence,
sin^2θ + cos^2θ = 1
Cosine Squared (cos²) Formula
The cosine squared is nothing but the cosine function multiplied by itself. The cos square theta formula can be represented as:
Cos^2θ
When the cosine function is squared, it finds its usage in a variety of new fields. It is particularly applied in the field of physics to compute calculations related to alternating current, finding the phase angle, calculating proportions, etc. It is also used in the field of circular symmetry to discern trends based on huge data in biology and geology. The squared cosine function is also used in statistics, especially in findings that involve data in the form of circles like compass readings. Another major application of the squared cosine function is processing signals and transmissions.
Cosine (cos) Formula Applications
The cosine (cos) formula finds a lot of uses in trigonometry as well as real-life tasks. Here are a few of those applications listed:
- The cosine formula is used in physics to determine vector components, simulate the mechanics of waves (both physical and electromagnetic), and oscillations, sum the strength of fields, and apply dot and cross products. The cosine formula is also used extensively in trigonometry to solve problems related to projectile motion.
- The cosine formula has applications in space flight and polar coordinates, music, ballistic trajectories, GPS, and cell phones.
- The cosine formula is also helpful in finding the height of existing buildings with triangles, designing trusses for roof support, and determining the ideal roof pitch for a house.
Have a look at the following examples where the cosine formula helps find the angles and side lengths of triangles:
- Find the angle θ of a right triangle with adjacent side = 6 cm and hypotenuse = 12 cm.
Solution: According to the cosine function;
Cos θ = adjacent side / hypotenuse
Cos θ = 6 / 12
Cos θ = 1 / 2
θ = 60 degrees
- Find the measure of the hypotenuse if the angle in a right triangle is 60 degrees, and the adjacent side is 10 cm in length.
Solution: According to the cosine function;
Cos θ = adjacent side / hypotenuse
Cos 60 = 10 / hypotenuse
½ = 10 / hypotenuse
Transposing the entities on either side of the equation, we get hypotenuse = 20 cm.
Cosine Squared (cos²) Formula Applications
The following are the practical applications of the cosine squared formula in trigonometric calculations:
- The cosine squared formula of trigonometry is used in solving problems that require you to calculate power in alternating currents.
- The cosine squared formula of trigonometry is used to process signals in navigation.
- The cosine squared formula of trigonometry can also be used to discern the trends and behavior of oscillating or periodic motion.
Have a look at the example below to know how to use the cosine squared formula:
Find cos^θ if sinθ = ⅘
Answer: We know that sin^2θ + cos^2θ = 1
So, cos^2θ = 1 – sin^2θ
cos^2θ = 1 – (⅘)^2
cos^2θ = 1 – 16/25
cos^2θ = 9/25
cosθ = 3/5
Using Cosine (cos) and Cosine Squared (cos²) in Trigonometric Identities
The cosine and cosine squared functions are significant components of various trigonometric identities. The angles and sides of a right triangle are represented by a unit circle using these identities. Given below are some examples of commonly used trigonometric identities involving the cosine and cosine squared functions:
- sin^2θ + cos^2θ = 1
- cos2θ = 2 cos^2θ – 1
- Cos θ = 1/Sec θ or Sec θ = 1/Cos θ
- Tan θ = Sin θ/Cos θ
- Cos (-θ) = Cos θ
- Cos (90 – θ) = Sin θ
- cos (180°- θ) = -cos θ
- cos(α+β)=cosα.cosβ–sinα.sinβ
- cos(α–β)=cosα.cosβ+sinα.sinβ
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ – sin2 θ = 2 cos2θ – 1 = 1 – 2sin2 θ
- cos (θ/2) = ±√(1 + cosθ)/2
- Cos A + Cos B = 2 Cos(A+B)/2 . Cos(A-B)/2
- Cos A – Cos B = -2 Sin(A+B)/2 . Sin(A-B)/2
- Cos A. Cos B = [Cos (A + B) + Cos (A – B)]/2
Graphical Representation
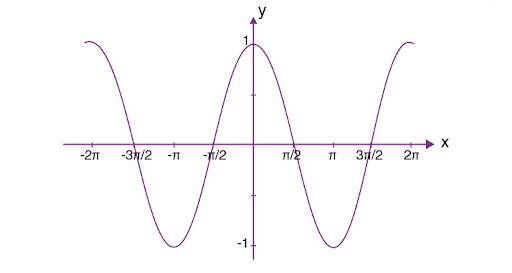
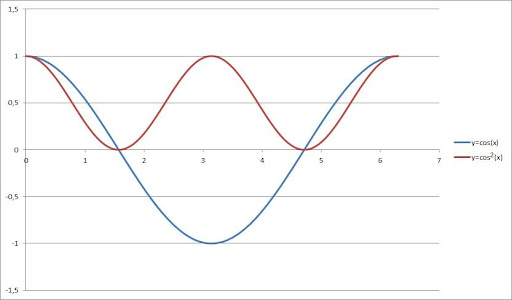
Here is the graphical representation of cosine (cos) and cosine squared (cos^2) on a coordinate plane:
Cosine (cos) Function
Cosine Squares (cos^2) Function
Periodic Nature of Cosine Function
The cosine function is periodic. In simpler words, the cosine function repeats itself after a particular interval. The cosine function has a period of 360 degrees or a full revolution.
Tips for Solving Trigonometric Problems
Have a look at some of the most effective tips while solving trigonometric problems mentioned below to avoid making mistakes at all times:
- Practice the trigonometric identities daily to get a hold of them and only use the most appropriate identity in any given problem to solve it efficiently.
- Learn the values for common trigonometric functions like cos 60, sin 90, etc. to avoid using the wrong values for wrong functions.
- Try to solve problems by visualizing a unit circle in mind for faster and fool-proof calculation.
- Do not ignore the signs in front of any number or function as signs can change the application of a function or an identity entirely.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- The cosine function represents the ratio of the angle of a right triangle to and the measure of the side adjacent to the hypotenuse (which is the longest side in a right triangle, facing opposite the right angle). The cosine function is used to solve a variety of problems that we face every day like finding particular angles and measure of distances.
- Mathematically, for any given angle, say θ, the cos function can be represented as Cos θ = measure of the side adjacent to the hypotenuse/ measure of the hypotenuse.
- The cosine squared is nothing but the cosine function multiplied by itself. It can be represented mathematically as Cos^2θ.
- The cosine function is used to solve a variety of problems that we face every day like finding particular angles and measure of distances. The same function when squared is mathematically represented as cos^2 and also comes in handy in an array of real-world scenarios such as problems relating to alternating current in physics and engineering, statistics, and more.
Quiz
Question comes here
Frequently Asked Questions
The cosine squared is nothing but the cosine function multiplied by itself. It can be represented mathematically as Cos^2θ
The cosine formula can be used to solve trigonometric problems which require you to find the length of undefined sides and angles.
The cosine squares formula is used in trigonometry to solve problems related to alternating currents, symmetry, oscillations periodic motion, and navigation.
Here are some examples of trigonometric identities involving cosine and cosine squared functions:
- sin^2θ + cos^2θ = 1
- cos2θ = 2 cos^2θ – 1
- Cos θ = 1/Sec θ or Sec θ = 1/Cos θ
- Tan θ = Sin θ/Cos θ
- Cos (-θ) = Cos θ
- Cos (90 – θ) = Sin θ
- cos (180°- θ) = -cos θ
- cos(α+β)=cosα.cosβ–sinα.sinβ
- cos(α–β)=cosα.cosβ+sinα.sinβ
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ – sin2 θ = 2 cos2θ – 1 = 1 – 2sin2 θ
- cos (θ/2) = ±√(1 + cosθ)/2
- Cos A + Cos B = 2 Cos(A+B)/2 . Cos(A-B)/2
- Cos A – Cos B = -2 Sin(A+B)/2 . Sin(A-B)/2
- Cos A. Cos B = [Cos (A + B) + Cos (A – B)]/2