
Mastering Trapezoid Area: Calculations Made Simple
Comprehensive Definition, Description, Examples & Rules
Introduction to Trapezoid Area
A trapezoid is a four-sided shape that consists of a pair of sides parallel to each other. A trapezoid is a two-dimensional shape similar to a rectangle or square, but it has most similarities with a parallelogram. A trapezoid also consists of a particular perimeter and area for itself, as the other shapes have.
Calculating the trapezoid area is important because:
- The trapezoid is one of the major disciplines of Calculus and is the most fundamental shape, so determining the area of a trapezoid is very important for mathematical calculations.
- Civil engineering requires calculating the area of different types of shapes, and a trapezoid is also one of the shapes that civil engineers can focus on while building anything, so calculating its area is important.
- In real-world applications, there are many situations in which calculating the area of a trapezoid can be important, as trapezoidal shapes are an important part of human life.
Understanding the Trapezoid
A trapezoid is a quadrilateral consisting of one pair of parallel opposite sides and is an important four-sided shape with two dimensions. A trapezoid has a lot of similarities with a parallelogram and is a very effective shape, which is important for mathematical calculations. The remaining two sides that are not parallel are known as legs, while the parallel sides are known as bases.
Characteristics of the Trapezoid
The Major characteristics of a trapezoid are:
- The bases of the trapezoids are parallel to one another.
- The median of the trapezoid is parallel to both the basis, and the length of the median will be the average of the length of the basis of the shape.
- The sum of all angles of the trapezoid will be equal to 360 degrees.
- Some of all angles of the trapezoid on the same side will equal 180 degrees.
The Trapezoid Area Formula
The area of a trapezoid formula is:
- A = (1/2) ×(a + b) × h
Here, the components of the formula of the area of the trapezoid are:
- ‘a’ and ‘b’ are the lengths of the two parallel bases of the trapezoid.
- ‘h’ is the height among the parallel bases of the trapezoid.
Finding the Area of a Trapezoid
The step-by-step instructions on how to calculate the area of a trapezoid is:
- You must know the lengths of the trapezoid’s two parallel sides (bases).
- Calculate the height of the trapezoid, which is also important to calculate the area of the trapezoid using the formula.
- Use the formula according to the BODMAS rule, and avoid making mistakes while calculating.
- The area of the trapezoid will be in square units.
Examples:
Calculate Area of Trapezoid with bases a = 10 cm, b = 14 cm, and height h = 8 cm.
Solution:
Area = (1/2) ×(a + b) × h
= (½)× (10+14) × 8
= 24/2 × 8
= 12 × 8
= 96 cm ²
So, the Area of the Trapezoid is 96 cm².
Special Cases: Finding Area Without Height
When calculating the area of the trapezoid, there will be situations where you cannot find the height of the trapezoid, as the height of the trapezoid will not be provided. In this situation, there is a particular method you need to follow that will help you calculate the exact area of the trapezoid by finding the length and the base of the non-parallel side.
In situations where the height of the trapezoid is not provided, you will divide the trapezoid into a congruent right-angle triangle and a rectangle and calculate area of trapezoid without height. By following this method, you will be able to calculate the height of the triangle. Still, it is a method that you can only apply for an isosceles trapezoid where the non-parallel sides of the trapezoid are also equal.
Real-World Applications
You can use the area of a trapezoid formula in your real-world application. There are various fields in which you can use it. These are:
- Architecture: The primary area where you can use the area of a trapezoid formula in real-world applications is the architecture field.
- Construction: The civil engineer has to do a lot of calculations, and while constructing, calculating the area of a trapezoid is also important.
- Geometry: Shapes are a primary part of geometry. A trapezoid is a shape with a lot of significance, and calculating the area of a trapezoid is an essential part of geometric calculation.
Infographics: Visual Representation
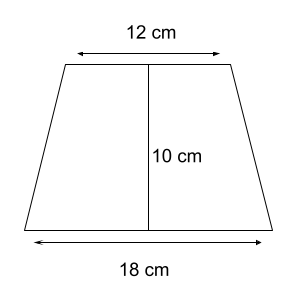
Find the Area of a Trapezoid with bases a = 12 cm, b = 18 cm, and height h = 10 cm.
Solution:
Area = (1/2) ×(a + b) × h
= (½)× (12+18) × 10
= 30/2 × 10
= 15 × 10
= 150 cm ²
So, the Area of the Trapezoid is 150 cm².
Common Mistakes and Pitfalls
The common errors that people can commit while calculating the trapezoid areas are:
- Determining the length of the two parallel bases is very important. While calculating, many people take the other sides rather than the parallel sides.
- There is a situation when it is important to calculate the height of the trapezoid where people mess up while the calculation happens.
- People think it is only possible to calculate the trapezoid area if the height is provided. Still, you need to divide the isosceles trapezoid into triangle and rectangle and then calculate the area accordingly.
To avoid mistakes while calculating the area of a trapezoid, the students need to follow the formula properly and use the BODMAS rule to get the exact area of the trapezoid answer.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- You need to determine the length of the two bases of the trapezoid and its height to calculate the area of a trapezoid.
- There are special cases in which you need to calculate the area of a trapezoid without its height.
- Following the BODMAS rule is a primary calculation of the area of a trapezoid.
- It is important to remember and use the formula effectively in the calculations.
Quiz
Question comes here
Frequently Asked Questions
There are situations where the height of the trapezoid will not be provided, and you need to calculate the area of that particular trapezoid. In that situation, you must divide the trapezoid into a right-angle triangle and a rectangle. Then, you can easily calculate the height of the trapezoid and then use the basic area of a trapezoid formula. It is possible to calculate the area of a trapezoid whose height is not given only if it is isosceles.
The area of a trapezoid is always calculated in square units. For Example:
- m²
- cm²
- km²
- ft²
No, there is only a special case where the height of the trapezoid might not be provided. Still, in that scenario, you need to calculate the height of the trapezoid and then use the general formula to calculate the area of a trapezoid. The basic formula is the only way to calculate the area of a trapezoid. There is a difficult option for you where you can avoid the formula when you can divide the trapezoid into a triangle and rectangle, calculate the area of each shape, and then add them up.
There are various real-world examples where, if you know the area of a trapezoid, it will be very useful. These are:
- Architecture is a major field in which if you know the formula for calculating the area of a trapezoid, it will help you to build things, and architects use a lot of shapes and areas in the building process.
- Civil engineers, while constructing, also require the area of a trapezoid formula that helps them determine the space they require to calculate for building a particular thing.
- Geometric calculations require a lot of shapes, and calculating the area of these shapes is also very important. One of the primary shapes that are the focus of the geometric calculations is the trapezoid.
The common mistakes to avoid while calculating the area of a trapezoid are:
- You need to write the area of a trapezoid in square units, which is one of the biggest mistakes people commit.
- Using the BODMAS rule for calculating the formula is essential, and people commit mistakes there.
- Messing of the formula is also a bigger problem, and you need to use the formula perfectly to calculate the accurate area of a trapezoid.
If you want to enjoy accurate results, check the examples mentioned in the blog and then take the Edulyte worksheet below, which will help you know your progress.

