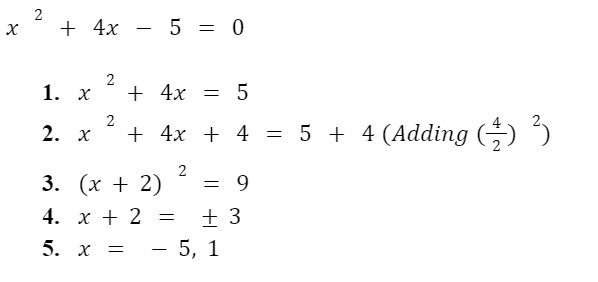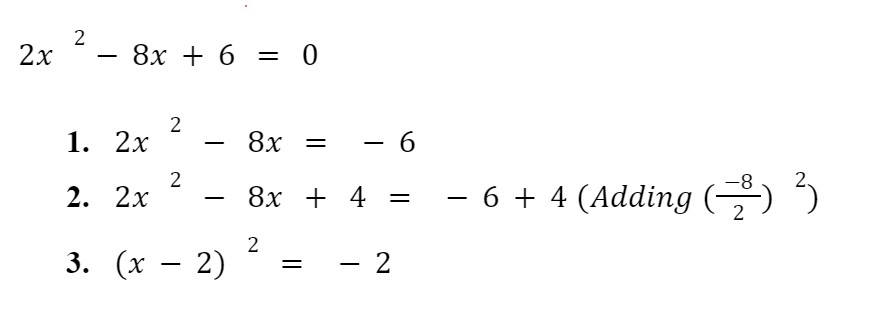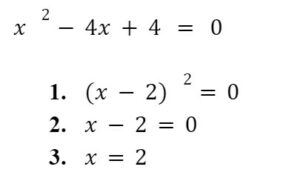Mastering Completing the Square: Methods, Formulas, and Examples
Comprehensive Definition, Description, Examples & Rules
Introduction to Completing the Square
Solving quadratic equations is one of the primary methods used in algebra, and it is done by completing the Square. Using this technique, one converts a quadratic equation into a perfect square trinomial to quickly determine its roots. It is a fundamental topic in math education because it shows how to decompose/group quadratic expressions, leading to further understanding.
Importance and Application
Solving with the completion of a square is used in different mathematics topics, from introductory algebra to calculus. It is important because it solves quadratic equations quickly instead of factoring or using the quadratic formula. However, this method is much more than an equation-solving routine. It is a path to understanding algebraic equations and how they work.
Complete the Square Formula and Steps
One of the essential expressions is completing the square formula, which turns a quadratic equation ax2+bx+c=0, and a=1 into a perfect square trinomial. The formula includes an integer, which is either added or subtracted to the binomial, giving a square. For the general quadratic equation, the completed square form is (x+b/2)2=(b/2)2−c.
Step-by-Step Breakdown
- Isolate the Quadratic Terms by beginning with a standard form quadratic equation.
- Moving the Constant Term to the Other Side: If ‘c’ is on the left side, move it to the right side of the equation.
- Factor Out the Coefficient of x2: Ensure that the coefficient of x2 is 1; if not, factor it out.
- Complete the Square by adding and subtracting b2a2 to the equation.
- Factor the Perfect Square Trinomial: Express the trinomial as x +b2a2.
- Solve for x by taking the square root of both sides and solving for x.
Illustrative Examples
Example 1: x2+6x+8=0
- x2+6x=-8
- x2+6x+9=-8+9 (Adding-422)
- (x+3)2 = 1
- x+3= 1
- x= -31
- x=-2 or x=-4
Example 2: 2×2 -4x-6=0
- 2×2- 4x = 6
- 2×2- 4x + 1 = 6 + 1 (Adding (-42)2)
- (x-1)2= 7
How to Complete the Square: Method and Examples
How to complete the square is subject to some minor changes in light of the kind of quadratic equation. Let’s explore the process for different scenarios:
Completing the Square for Basic Quadratic Equations With Completing the Square Examples:
Scenario 1: Quadratic Equation with Leading Coefficient a=1:
Scenario 2: Quadratic Equation with Leading Coefficient a 1:
Completing the Square for Special Cases With Completing the Square Examples
Scenario 3: Quadratic Equation with Perfect Square Trinomial:
Scenario 4: Quadratic Equation with Constant Term Only:
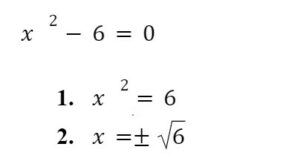
Factoring by Completing the Square
Complete the square formula is helpful for more than just solving quadratic equations. In factoring by completing the Square, a quadratic expression is transformed into the Square of a binomial. This technique is precious where conventional factoring techniques like the quadratic formula prove inscrutable.
Examples Showcasing Factoring by Completing the Square
Example 1: x² + 8x+16
- (x+4)²
Example 2: 2x²-12x+18
- 2 (x-3)²
Complete the Square Method for factoring is not only helpful to solving the problems but understanding how quadratic equations are structured.
Mastering Completing the Square: Tips and Techniques
Completing the square steps involves both grasping the fundamental concepts thereof as well as performing it repeatedly. Here are some tips and techniques to enhance proficiency:
- Understand the Quadratic Form: You should also be keen to ensure that the quadratic equation is transformed into standard form i.e. (ax2+bx+c=0)
- Isolate the Quadratic Terms: First, pull out the quadratic terms to one side of the equation.
- Factor the Coefficient of x2: Factor out the expression if the coefficient of x2 is not 1.
- Complete the Square: Take away and add the square of half of the value of x to get a perfect square trinomial.
- Factor the Perfect Square Trinomial: Change the expression into a square of a binomial.
- Solve for x: Solve for x after taking the square root on both sides.
Common Mistakes to Avoid while Completing the Square Steps
- Forgetting to Factor the Coefficient of x2: First, always divide out by the x2 term before completing the square.
- Neglecting the Constant Term: You must include the constant term in completing the Square to avoid getting wrong answers.
- Misapplying Signs: Caution should be taken with signs while adding and subtracting terms during the completion of the Square.
- Skipping Steps: The steps taken should always be noticed because each step leads to more accuracy in the final solution.
Applications of Completing the Square
Solving a quadratic equation is one of many achievements of completing the Square Formula. Through understanding and applying this method, one develops skills in different mathematical concepts and everyday situations.
Real-World Examples
- Physics: Physics is central while solving motion equations; in the case of the projectile motion and the parabolic paths, one should begin by completing the Square.
- Engineering: Engineers use completing the Square in structural analysis and optimization problems where quadratic equations model physical systems.
- Computer Graphics: Precise and smooth rendering of shapes and curves in computer graphics often requires completing a square, thus making it possible to perform computations efficiently.
- Economics: Such quadratic equations are found in economic models, and completing the Square can help analyze and improve these models.
- Statistics: In statistical regression analysis, we frequently utilize the concept of completing the Square as we may have quadratic functions.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- Completing the Square Fundamentals: Transforming quadratic equations into easily manipulated forms and finding square roots. In math education, it is essential to understand quadratics.
- Formula and Steps Breakdown: Apply the completing the square approach by separating terms, transferring constants, and solving xx.
- Versatility in Technique: Factoring and writing expressions as binomial squares.
- Tips for Mastery: Avoiding the wrong ones helps to get it right.
- Real-world applications: Physics, engineering, computer graphics, economics, and statistics (practical use).
Quiz
Question comes here
Frequently Asked Questions
Completing the square involves several steps:
- Isolate the quadratic terms.
- Transpose of the constant term to the other side.
- Factor the coefficient of x².
- Complete the square by adding and subtracting (b2a)².
- Factor the perfect square trinomial.
- Consider square roots from each side and solve for x
The step-by-step process is as follows:
- Isolate the Quadratic Terms
- Take the Constant Term to the other side.
- Factor the Coefficient of x²
- Complete the Square
- Factor the Perfect Square Trinomial
- Solve for x
- Solving Quadratic Equations: An alternative technique known as completing the Square is available for solving quadratic equations, most times when factoring or the quadratic formula are less valuable.
- Factoring Quadratic Expressions: It assists in factoring quadratic expressions, enabling one to understand their features.
- Broader Applications: Knowledge of the “completing the square” technique helps hone problem-solving skills in many areas, including physics and computer graphics.
Completing the Square converts a quadratic expression into the Square of a binomial, simplifying the factoring process. This approach is a straight way of factoring and is often useful when conventional techniques take work.
Completing the Square has real-life applications in physics, engineering, computer graphics, economics, etc. It is an all-purpose device used to model and solve real-life problems relating to quadratic relations.