Understanding Cones: Shapes, Formulas, and Properties
Comprehensive Definition, Description, Examples & Rules
Introduction to Cones
A cone is a particular shape formed by using a set of line segments or particular lines that can connect a common point called a vertex or Apex point to all the points of a circular base. The distance from the cone’s vertex to its base is known as the height of the cone. A cone can be expressed as a three-dimensional shape by nature.
Characteristics
The major characteristics of a cone are:
- It consists of one circular base.
- A cone consists of zero edges.
- It has one vertex (corner).
- The point from the vertex to the center of the circular base is calculated to be the height of the cone.
Basic Properties of Cones
There are certain properties of a cone that make it one of the most special shapes indeed. The properties are:
- Circular Base: A major property of a cone is it consists of a circular base similar to that of a cylinder, and the circular base is the base, which makes the cone a special shape for calculating mathematical equations.
- Apex: The apex, or vertex, is the highest point of a cone where the lines from the circular base intersect. The height of the cone is measured from this apex to the center of the circular base.
- Slant Height: In addition to the vertical height, cones have another important measurement called the slant height. The slant height is the distance from the apex of the cone to one of the edges of its circular base. It is specifically calculated for three-dimensional shapes.
- Height: The height of the cone here is considered as the vertical height of the cone, which is directly calculated when you calculate the distance from the apex or the vertex of the cone directly to the center point of the circular base of the cone, which will be considered as the overall height of the shape of a cone.
The formula for Calculating Cone Volume
The formula is:
- V = (⅓)πr²h
For step-by-step calculation:
- It is in cubic units.
- ‘r’ is radius.
- ‘h’ is height.
The Formula for Calculating Cone Surface Area
The formula for cone that you have to use for calculating the surface area of a cone is:
- Total Surface Area = πr (r + L)
Here, ‘r’ is commonly the radius of the cone’s circular base.
‘L’ can be denoted as the slant height of the cone, which is the height of the cone from the apex to one of the edges of the circular base.
Example
Calculate the total surface area of a cone with a radius of 5 cm and a slant height of 7 cm using π = 22/7
Solution:
The formula is:
πr (r + L)
π 5 (5 + 7)
22/7 × 60
188.57.
So, the total surface area of the cone is 188.57 cm².
Types of Cones
You use various types of cones for mathematical equations, and all these cones are very important for calculation. The types of these cones are:
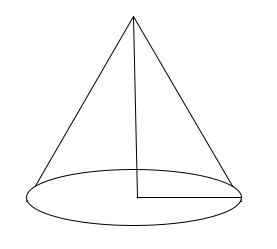
Right Cones
A right cone has its Axis perpendicular to that of the plane of the base, and you can generate a right cone by revolving a right triangle through one of its edges. The diagram of the right cone is as follows:
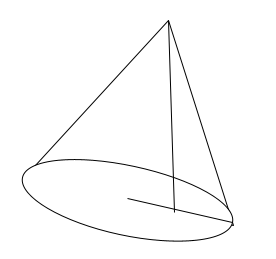
Oblique Cone
A cone with a circular base, but the axis of that particular cone is not perpendicular to that of the base will then be called an oblique cone. The vertex of a particular cone is not located directly above the center of the circular base. The diagram to support the oblique cone is.
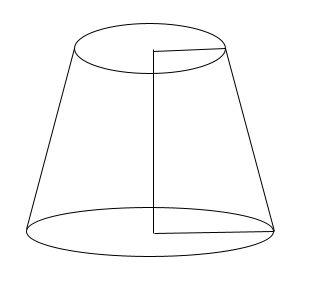
Truncated Cones
A truncated cone is a cone that lacks an Apex and the terminating clean in a usually parallel length to the base. It is one of the most uncommon shapes of a cone, and the diagram to define the shape is as follows:
Cone 3D Shape
A cone itself is considered a three-dimensional nature shape as one of the major elements of the cone is its radius height and slant height, which makes it a three-dimensional shape. It can be generally considered as a flat and curved surface pointed towards the top, and the joining point of the curve makes it a three-dimensional shape, giving it a three-dimensional nature.
The geometry of a cone is three-dimensional as the height radius and slant height is a major part of the geometry and makes it geometrically a perfect 3D shape.
The appearance of a cone is 3D. As you might have seen in the above diagrams, all the shapes are formed by three dimensions where you can easily identify the cone’s circular base.
Equation of a Cone
Various mathematical equations of a cone represent its various forms and how to use them in your mathematical calculations. The various cone equation that you have to keep in mind are:
- Slant height: l = √(r² + h²)
- Total Surface Area: TSA = πr (r + l)
- Curved Surface Area: πrl
- Volume with Height and Radius: V = (⅓)πr²h
- Volume with Height and Diameter: V = (1/12)πd²h
- Volume with Slant Height: V = (1/3)πr2h = (1/3)πr2√(L2 – r2).
These are the cones formulas.
Real-world Applications of Cones
The usage of the cones in real-world applications are:\
- Ice cream Cones: One common example of a cone is an ice cream cone, which we encounter regularly in our daily lives. This familiar object directly compares to the shape we are discussing in this blog.
- Traffic Cones: A traffic cone is a cone shape that we use regularly in our lives.
Calculating the Length of a Cone
The length of a cone can be calculated using the Pythagoras Theorem, which you have to use to calculate the slant height of a cone, which will be the length of your cone. You have to measure the height and radius of your cone for your calculations.
Step Up Your Math Game Today!
Free sign-up for a personalised dashboard, learning tools, and unlimited possibilities!

Key Takeaways
- A cone is a 3D shape that consists of a circular base.
- The Slant height of the base is an important property that calculates its volume and surface area.
- Calculating the cone is possible when you use the Pythagoras Theorem to calculate its length.
Quiz
Question comes here
Frequently Asked Questions
There are two surface areas: the total and the curved surface areas. The formula includes:
- Total Surface Area: TSA = πr (r + l)
- Curved Surface Area: πrl
To calculate the length of a cone, including its length height, you have to use the Pythagoras Theorem and calculate the height and radius of the cone, which will allow you to find out the slant height of the cone using the basic formula you can easily find the length of your cone by finding out the slant length of the shape.
You can geometrically define a corner to be a three-dimensional geometric shape with a smooth, flat base and a circular base, which joins to the point of the apex and creates the height of the cone. You actually can geometrically define a cone to be a perfect three-dimensional shape.
Certain interesting facts about the cones are:
- It consists of zero edges.
- It consists of a circular base.
- It has a single vertex or a single corner.
- The point at which the vertex of the cone joints center of a circular base is called the height.